The equilibrium dissociation mole fraction of NH_3 as a function of temperature T and Pressure P can be calculated from the standard free energy change DeltaG° and the equilibrium constant k. The standard free energy change for the reaction
(34) ![]()
is given by (Ref. 26):
(35) ![]()
The equilibrium constant can therefore be written as:
(36) ![]()
From the stoichiometry of the reaction, decomposition of 1 mole of NH_3 produces 3/2 y moles of H_2, 1/2 y moles of N_2, and (1-y) moles of NH_3. Making the substitution y=2x to simplify calculations the total moles are written as
(37) ![]()
and the partial pressures are
(38) ![]()
In terms of partial pressures the equilibrium constant is written as
(39) 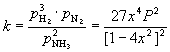
and solving for x yields
(40) 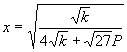
where k is given by equation (36). The decomposed mole fraction f is given by:
(41) 
Figure 13 shows the decomposition fraction of NH_3 in the jet nozzle reservoir as a function of temperature T_o at different pressures P_o. It is assumed that the nozzle reservoir can be approximated as a closed container of constant pressure and temperature without any net gas flow, which is true if the nozzle is much smaller than the gas inlet being much smaller than the nozzle reservoir. As can be seen the decomposition is smaller at higher pressures and lower temperatures (Le Chatelier's principle).
When the NH_3 gas exits through the nozzle into free space the gas expands and the pressure is reduced as well as the temperature as discussed earlier in the chapter on jet theory. Let us assume that the reaction given by equation (34) is at complete equilibrium when the gas crosses the quitting surface, which marks the point where viscous flow turns into molecular flow. This means any further interaction of particles can be neglected. As discussed earlier, any thermodynamic property of the continuous jet can be determined, like pressure and temperature, if the Mach number M at the point of interest is known. This is a good example where this comes in handy.
The terminal Mach number, which is reached at the quitting surface, is calculated by combining equations (6), (9), and (1) to get:
(42) 
where for NH_3 A=(about)0.9, B=(about)0.3, g=1.33, sigma=(about)2.2 Å, and d is the nozzle diameter of the jet. The reduced pressure and temperature can be computed by using equation (111), which allows the determination of pressure P and temperature T in terms of the Mach number M, and is repeated here:
(43) ![]()
These pressures and temperatures can then be used in equation (41) to determine the decomposition fraction.
Figure 14 shows the decomposition as a function of T_o and P_o for the NH_3 jet prototype #2 using d=200 mm and a solid sphere cross section of sigma=2.2Å, equal to the approximate molecular radius of ammonia . For example, at a typical nozzle pressure of P_o=80 torr, significant decomposition occurs at approximately 600°C.
In summary the decomposition depends on the validity of the quitting surface model and terminal Mach number approximation, as well as the assumption that the reaction rate is much larger than it takes the NH_3 to reach the quitting surface. At low temperatures though the reaction rate is very low, as can easily be recognized noting that pure N_2/H_2 mixtures as well as NH_3 are available in gas cylinders, without reacting to equilibrium at any reasonable rate. Further, industry uses catalysts (like Fe) to obtain NH_3 from N_2 and H_2 at any reasonable rate. More experimental efforts are needed to verify the decomposition fraction as a function of nozzle pressure P_o and nozzle temperature T_o. It should be possible to determine the approximate temperature at a given nozzle pressure where the decomposition rises sharply as shown in Figure 14 by observing the N_2 peak of a Residual Gas Analyzer (RGA). It should be recognized though that the decomposed NH3 fraction in the `beam' is very dependent on physical conditions of the gas delivery system, since at low and medium temperatures NH_3 and decomposed NH_3 (N_2 and H_2) will mix in the gas handling system, and equilibrium will never be reached in the nozzle. Reproducible experimental results are therefore only expected if all parameters are kept the same (valves are opened the same amount every time, etc.) and sufficient time is provided for the gas to mix to a steady state in the gas handling system.
Figure 13: Decomposition Fraction of NH_3 in Jet Nozzle Reservoir (Note: Mistake in Graph. X-axis is Celsius, not Kelvin)
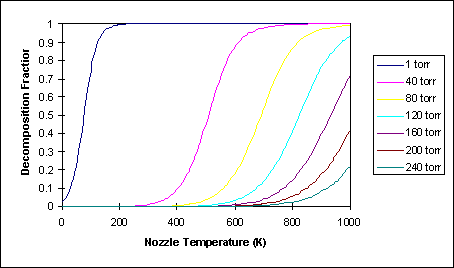
Figure 14: Decomposition Fraction of NH_3 for d=200 mm, sigma=2.20 Å
Table of Contents