The intensity I_j due to the jet can be calculated as follows. The ideal intensity I_o was calculated by using equation (13) in conjunction with (14) and the ideal gas law (1). The transmission coefficient lambda_s due to skimmer and wall effects was calculated using equation (15) in combination with equations (9), (1), (6), and (11). Beer's law attenuation coefficient lambda_b was calculated by using equation (16) with l=x_s-x_q together with the ideal gas law valid in the region between the nozzle and the skimmer
(24) ![]()
and using equation (4) for P_b. The resulting intensity I_j can then be obtained using
(25) ![]()
The intensity I_b due to the background pressure P_b escaping through the skimmer aperture can be calculated using equation (17) in conjunction with equation (4).
To convert the intensities from (molecules / sr s) to (molecules / cm^2 s) to obtain the fluxes at the substrate the intensity is divide by the length of travel squared. Therefore:
(26) ![]()
and
(27) ![]()
Next the issue of fluxmeter readout has to be dealt with. Our fluxmeter is a standard HV Bayard-Alpert ionization gauge which reads densities. The conversion between flux and density is given by:
(28) ![]()
where V_j is given by equation (2) in conjunction with (3) and V_b is given by:
(29) ![]()
Next the conversion from density rho to ion gauge pressure readout G using the ideal gas law is used:
(30) ![]()
where g is the sensitivity factor for NH_3 relative to N_2 which can be approximated by using the electron scattering cross section relative to N_2 squared. This value is approximately g=0.56. The multiplication factor t takes care of the problem that our fluxmeter does not measure the particle density that would normally pass through it if the fluxmeter would be open on both ends. Since the fluxmeter is closed at the back as well as having an opening on the top leading into the sample manipulation mechanism there is no practical way in obtaining the factor t directly unless the gauge can be calibrated using RHEED oscillations in conjunction with a known sticking coefficient. This is due to the fact that the flux leaving the detector is unknown as well as the change in velocity and the fraction of particles sticking to surfaces inside the gauge. Therefore the value t was fitted recognizing that in the equilibrium state the readout G is a linear function of velocity V and flux I. The total pressure on the readout is given by:
(31) ![]()
The parameters used and results obtained for the peak flux are shown in Table 6 and Figure 9. A multiplication factor b has been used to correlate the real background pressure with the measured background pressure in Figure 9b, which is probably much lower due to the long and narrow duct leading to the ion gauge and pumping due to the turbo pump.
The parameters used to get a good fit resulted in an effective pumping speed of 2.45 l/s and a solid sphere cross section s of 0.95 Å. The fitting parameter t for the fluxmeter was 19. Both the effective pumping speed and cross section giving the best fit are much lower than would be expected. This suggests that the model used might not be applicable, mainly due to the unknown background pressure P_b and the unknown dissociation fraction of NH_3. Both issues could be addressed much easier with a redesigned jet suggested in another section, which also covers the current limitations.
It is worthwhile noting that lambda_s=1 due to the fact that r>>x_q<<x_s, and, due to reasons mentioned before, r>>d. Therefore the jet intensity I_j can be written as
(32) 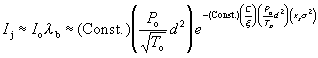
or, using the mean free path l_m, as:
(33) 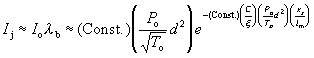
to easier follow the dependence of the jet intensity I_j on the jet and operating parameters. Note that C/xi and sigma^2 can not be combined in one fitting parameter due to the fact that the background intensity I_b also depends on C/xi. By looking at graphs similar to Figure 9 using the preceding parameters it is observed that decreasing the nozzle to skimmer distance x_s from 1.3 cm to 0.65 cm the jet flux I_j increases by a factor of about 2. The same happens by doubling the pumping speed xi. Reducing the nozzle diameter d from 200 mm to 100 mm has little effect on the jet intensity except that the peak shifts to about P_o=135 torr and is much broader. Increasing the nozzle temperature T_o from 373 K to 473 K results in only a slight increase in intensity, 1273 K approximately doubles it. This shows the importance of a small nozzle to skimmer distance x_s to minimize attenuation due to the background pressure P_b as well as the use of a pumping arrangement with a high pumping speed xi to reduce P_b.
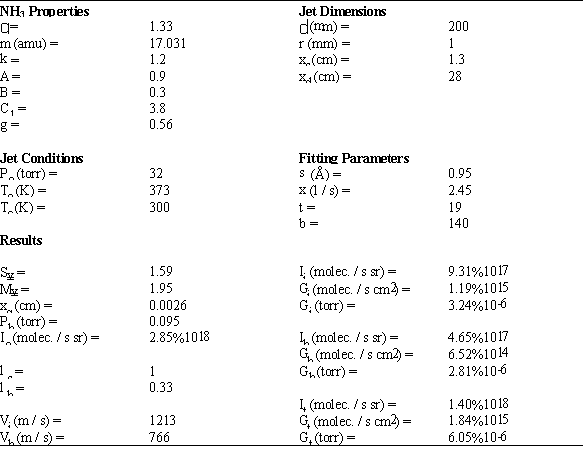
Table 6: Results for NH_3 Jet Prototype #1
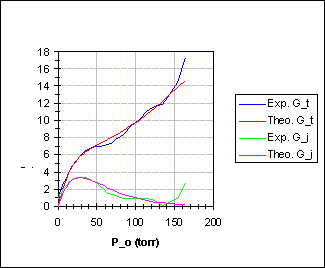
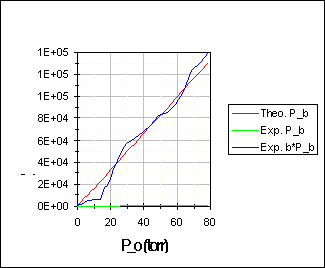
Figure 9: Jet Intensity and Background Intensity Characterization for the NH_3 Jet Prototype #1
Table of Contents