(5) ![]()
Therefore S_(infinity)is a measure of the thermal spread in the terminal translational velocity, the higher the value the more monochromatic the beam. Alternatively the terminal Mach number M¥ is often used as a parameter to describe this spread, and has a fixed relationship to the terminal speed ratio V_(infinity) (based on a velocity distribution function in the noncontinuum region, see appendix) given by
(6) 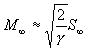
based on the fact that the terminal Mach number is defined as the terminal translational velocity V_(infinity) over the local speed of sound a in the reference frame of the moving "beam":
(7) ![]()
It should be emphasized that the terminal speed ratio S_(infinity)as well as the terminal Mach number M_(infinity) have nothing to do with the terminal translational velocity (or energy) V_(infinity) of the gas molecules, which depend only on the initial gas temperature T_o and the gas specie used. The terminal speed ratio S_(infinity) and terminal Mach number M_(infinity) only describe the velocity dispersion V_(parallel),_(infinity),_(thermal) of the "beam".
The terminal speed ratio can be calculated using
(8) 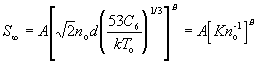
or, using a solid sphere cross section (in case of a heated jet):
(9) ![]()
where A and B are given in Table 4 and C_6/k=4(epsilon_p/k)sigma_p^6 is given by Table 3. Note that epsilon_p and rho_p come from pseudopotential calculations and that the cross section (53C_6/kT_o)^(1/3) has been written in a form such that it may be replaced by pi sigma^2, a hard-sphere cross section, if it is necessary to estimate S_(infinity) for expansion from heated sources. The parameters given are from a theoretical model; for monatomic gases, the parameter values derived from experimental fits are also given in Table 4. The results from polyatomic molecules are less reliable, but should be adequate for diatomics, such as nitrogen (N_2), carbon dioxide (CO), or Oxygen (O_2), where vibrational relaxation can be neglected and rotational relaxation occurs far out in the expansion close to where translation relaxation occurs (Ref. 21).
Although the correlation predicts the terminal speed ratio, it can be used to approximate the terminal temperature( see appendix):
(10) 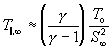
While the previously described correlations can be used to estimate S_(infinity) or T_(parallel),_(infinity) for polyatomics, these quantities are less reliable than in the case of monoatomics. The difficulty is that two relaxation processes (internal and translational) - that is, two cross sections - are involved and a single, simple correlation cannot be sufficient.
The location of the quitting surface from the nozzle can be estimated using:
(11) 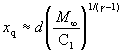
where C_1 depends on gamma which is given in Table 5. This comes in handy to ensure that the quitting surface is located between nozzle and skimmer so that the skimmer is placed in the molecular flow region.
The velocity dispersion V_(parallel),_(infinity),_(thermal) parallel to the mass flow speed V_(infinity) can be calculated using:
(12) 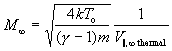

Table 4: Terminal Speed Ratio Correlation (Ref. 21), Equation
(132)
* Experimental fits for g = 5/3

Table 5: Constant for Quitting Surface Distance
Table of Contents