Figure 3 shows a typical supersonic jet expansion under our operating conditions. The gas is initially contained in the nozzle reservoir and kept at an initial temperature T_o and pressure P_o. The accelerating flow can be approximated as an isentropic flow, with neglectible viscous and heat conduction effect. The gas starts from a neglectible small velocity, called the stagnation state (P_o, T_o). An imposed pressure difference (P_o-P_b) accelerates, as the area of the nozzle decreases, the gas towards the source exit.
The gas expands through the nozzle passing the continuum flow region, crossing the quitting surface, and continuing in the molecular flow region until encountering the wall and skimmer. The skimmer selects part of the "beam" which proceeds towards the target or sample. Molecules not passing the skimmer are reflected back and contribute to the background pressure P_b in the region between nozzle and skimmer, which is pumped to keep the pressure as low as possible to minimize attenuation of the forward directed molecules coming from the quitting surface.
The "beam" is said to be supersonic if the ratio of nozzle pressure P_o to the background pressure P_b exceeds a critical value of about 2, always the case in our jets, which causes the translational velocity of the beam to exceed the local speed of sound in the continuum flow region. It should be mentioned that at the nozzle exit the translational velocity always equals the local speed of sound independent of nozzle conditions, characterized by a Mach number M=1, as indicated in Figure 3. This is true as long as the nozzle pressure P_o exceeds the background pressure P_b and the pressure in the nozzle is high enough to allow for a continuum expansion through the nozzle.
The continuum flow region is a region in which the gas density and collision frequency is high enough so that local equilibrium of the temperature components parallel and perpendicular to the beam is maintained, T_(parallel)=T_b. The quitting surface is an estimation on where continuum flow ceases and molecular collisionless flow begins (molecular flow region). It is not to be taken literally since the transition from continuum to molecular flow is gradual. Note the absence of shock waves which are very common to supersonic expansions. This is due to the fact that the background pressure P_b is kept at a low enough value so that the continuum expansion does not have to adjust for boundary conditions imposed by Pb which results in the occurrence of shock waves. Also, keeping P_b at a low enough value causes the quitting surface to be located close to the nozzle so that the skimmer is positioned in the molecular flow region. It should be mentioned that the nozzle shape has only little effect on the expansion in terms of properties discussed.
The molecular flow is typically affected strongly by the surroundings. First, Beer's law of attenuation by the background gas pressure P_b has to be considered. Second, jet molecules reflected off surfaces placed in front of the expansion play an important role under certain conditions. This effect can be quite large and therefore the skimmer and the wall separating the free jet source chamber from the beam utilization chamber has to be considered as discussed later. It turns out though that this effect can be neglected for jets designed by our group.
The Mach number M is also used to calculate thermodynamic properties in the continuum expansion region. Once the Mach number M is known, all thermodynamic variables can be computed. This is the reason why M is used as a universal parameter in characterizing jets. The Mach number M can be computed from fluid mechanics and has to be solved numerically for supersonic expansions. Since the continuum region is of less interest to us it is covered in the appendix. Note that the Mach number M has nothing to do with the translational velocity of the molecules, which only depend on T_o and the gas specie used.
A beam of a gas from a supersonic jet can be characterized by several parameters. Of most interest to us so far were the terminal translational velocity V_(infinity) (also called mass flow speed or translational energy), the parallel terminal thermal speed dispersion V_(parallel),_(infinity) thermal, and the intensity of the "beam" due to the jet, I_j, as well as the intensity due to the background pressure P_b between skimmer and nozzle, I_b. The dissociation fraction for NH_3 will be covered in another chapter, as well as the "seeding" effect due to NH_3 dissociating. Clustering of the gas specie used is another concern in gas expansions due to the substantial cooling of the gas, which does not seem to be a problem in our jets.

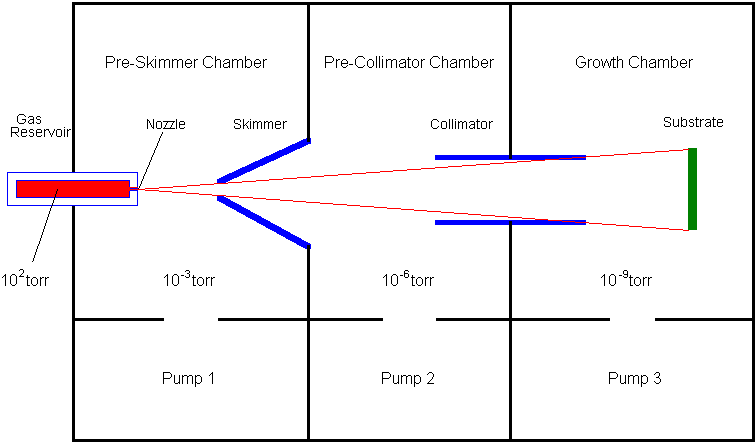
Figure 2: Typical Layout of a Supersonic Jet

Figure 3: Typical Jet Expansion
Table of Contents