The ideal free-jet centerline intensity per steradian can be conveniently expressed in terms of the nozzle flow rate, N(dot), and a peaking factor, kappa, given in Table 14.
(135) ![]()
where N(dot) is determined by using
(136) ![]()
The peaking factor kappa of an effusive source, i.e. free molecular flow from a thin walled orifice, is equal to 1, which is the reason for adding the factor pi (sr) in equation (135). The peaking factor kappa was determined by numerical solution of the hyperbolic differential equations describing the flow downstream of the sonic plane (Ref. 60).
It is hard to obtain m(dot) due to the fact that the subsonic flow in the nozzle is compressible and viscous effects are important in a thin region, called the boundary layer, near the walls of the nozzle. For short nozzles at high flow rates this viscous region does not effect the core of the flow and can be approximated as a quasi one-dimensional compressible flow (Ref. 21). The cross sectional area of this core region is close to the cross sectional area of the nozzle. This is true for converging nozzles and can be used with confidence for capillary nozzles for the jet properties of interest to us as discussed earlier. The flow is assumed to be a reversible and adiabatic process, and thus the state of the gas changes isentropically. In the sonic exit plane the flow is assumed to be homogeneous and parallel over the circular nozzle exit (Ref. 60). This approximation assumes that flow properties, such as M, are constant across any cross section of the nozzle, and m(dot) can be obtained by integrating equation (113) to get
(137) ![]()
Combining equations (108), (109), (112), (137), and the ideal gas law with the assumption that M=1 at the nozzle exit yields
(138) 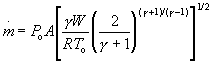
where A is the "throat" or minimum area of the nozzle and is equal to pi d^2 /4. As mentioned earlier, ones the flow becomes supersonic all isentropic properties are independent of the background pressure P_b as shown by equation (138). Substitution of equation (138) into (136) yields
(139) ![]()
with F(gamma) defined as
(140) 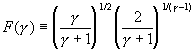
The ideal intensity I_o is therefore finally given by substitution of equation (139) into (135) to yield:
(141) ![]()
Theoretical values for F calculated using equation (140) and theoretical values for kappa are given in Table 14. This result can be compared to an effusive source. Assuming a Knudsen cell62, the intensity from such a cell (Ref. 62) is given by:
(142) 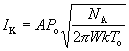
Using the ideal gas law and rearranging, the intensity can be written as:
(143) ![]()
Concerning the center-line intensity, the major advantage of a supersonic expansion is the high flow rate per unit area achievable compared to an effusive source, and not the peaked flow pattern, as for polyatomic gases kappa approaches 1 (same as for an effusive source). Comparing equation (141) and (143), the factor kappa F(gamma) in a jet source is replaced by the constant value 0.282 for an effusive source. For the same flow rate, the centerline intensity for a free jet source is at best (for gamma = 5/3) a factor of
(144) ![]()
better than the effusive source. For NH_3 (gamma=1.33) this factor is approximately 2. Therefore, the high intensity realized in free jet sources is due to large N(dot) (large P_o, d, and/or T_o using large pumps to reduce P_b) values and not the peaking factor kappa. The experimental results agree well with these predictions (Ref. 21). Neglecting background scattering, these isentropic results for I_o are also valid far out in the noncontinuum expansion. This is true because the intensity falls as 1/r^2 both in continuum and free-molecular regimens and the mean velocity V is established at small distances (Ref. 21). The intensity of the beam is usually limited by the source region pumping speed as suggested by Sibener et. al. (Ref. 65) and discussed later. In the concluding section of this chapter a leak valve will be compared to a supersonic jet in terms of achievable beam intensity and gas load on the system.
For diffusion pumped systems, a convenient expression for the attenuation of the centerline intensity at the detector relative to the ideal I_o is (Ref. 61)
(145) 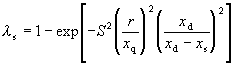
where S is taken to be the continuum speed ratio at the quitting surface usually estimated by S_infinity given by equation (132), that is, the terminal speed ratio. Note that r is the radius of the skimmer aperture, and x_q, x_s, and x_d are the location of the quitting surface, the skimmer, and the detector, respectively. This expression assumes x_s>x_q, (x_d - x_s)>>r, and S > 5, and neglects background gas scattering. The second term is a measure of the effectiveness of the wall between the source and the beam utilization chamber in blocking molecules leaving the quitting surface. Note that as x_d goes to x_s, then I goes to I_o, as expected. A simple design rule can be found using a virtual source distribution function (Ref. 60) which states that for lambda_s>0.9, r/d>20 for gases of gamma=5/3, and r/d>40 for gases of gamma>7/5, which is true for our jets.
To additionally account for background gas scattering Beer's law of attenuation is used:
(146) ![]()
where the total cross section, Q, often expressed as pi sigma^2, must be carefully considered. The result of scattering in diffusion pumped systems normally provides for a gradual fall off in intensity beyond the maximum (MM - maximum maximorum), as shown in Figure 4, and therefore the skimmer position is more often determined by the desired beam divergence, or some other geometrical constraint, or by the allowable flux into the beam utilization chamber.
Figure 4 shows the qualitative behavior of detector intensity I versus source pressure P_o for a fixed geometry. A plot of terminal speed ratio would look qualitatively similar except that the speed ratio continues to increase in the region where the intensity has leveled off (Ref. 21). The speed ratio then levels off and falls, but at significantly higher source pressures P_o. The basis for this behavior is that the initial scattering attenuates the velocity distribution uniformly, since the velocity dependence of the scattering cross section is small over the spread in velocities of most free jet. Hence, if one desires a high speed ratio for velocity resolution, it is often expedient to operate in the region where the intensity has leveled off, or even reduced.
The intensity I_b due to the background pressure P_b escaping through the skimmer aperture can be calculated assuming a Knudsen cell. A Knudsen cell calculation can be used if the radius r of the orifice, in this case the skimmer aperture, is about 1/10th or less of the mean free path of the gas molecules at the equilibrium pressure P_b, and the wall around the orifice is vanishing thin (good skimmer) so that gas particles leaving the enclosure are not scattered or absorbed and desorbed by the orifice wall. Assuming that P_b is much smaller than the pressure in the beam utilization chamber and looking only at the centerline intensity the Knudsen equation can be written as (Ref. 62):
(147) 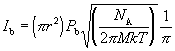
The background pressure P_b needed in equation (146) and (147) can be calculated considering the mass balance equation
(148) ![]()
The molecules leaving through the skimmer due to the jet beam can be neglected since
(149) ![]()
The about sign was used since the area suspended by the skimmer aperture on the solid angle surface is approximately the area of the skimmer aperture since d<<x_s. Similar the molecules leaving through the skimmer due to the background pressure P_b are neglected since the area of the skimmer aperture is usually much smaller than the "pumping area". Therefore it is justified to write:
(150) ![]()
The molecules per second pumped can be calculated by using
(151) ![]()
where xi is the pumping speed in volume per second. Using the ideal gas law and solving for P_b yields:
(152) ![]()

Table 14: Intensity Parameters (Ref. 21)
Table of Contents