The quantitative analysis of the noncontinuum regimen requires the solution of the Boltzmann equation and is not straightforward (Ref. 21). At sufficiently large collision rates the distribution of velocities about the mean velocity V is isentropic and a local equilibrium temperature, T, is related to T_parallel and T_perpendicular by:
(124) ![]()
Therefore, in the continuum region the collision frequency is sufficient to maintain local equilibrium T_parallel=T_perpendicular. On the other hand, the terminal values for the temperatures T_parallel,_infinity and T_parallel,_perpendicular are not as easily related due to the fact that the collision frequency is too low far out in the expansion to maintain local equilibrium T_parallel=T_perpendicular. Note also that because of parallel collisions constant scattering of molecules into the perpendicular directions takes place contributing in altering the gaussian velocity distribution to become non-gaussian. Based on a velocity distribution function covered by Miller et. al. an effective terminal temperature can be approximated as:
(125) ![]()
The terminal (parallel) Mach number M_infinity (see equation (106)), using k=R/N_A,
(126) 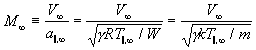
continues to be used as the parameter characterizing the continuum expansion, although the terminal speed ratio, that is, the mean terminal velocity V_infinity (mass flow speed) divided by the terminal parallel thermal spread in velocity V_parallel,_perpendicular,_thermal parallel to the mean mass flow
(127) ![]()
is more directly related to beam resolution. Note that V_parallel,_infinity,_thermal, using equation (125), is defined as
(128) ![]()
or:
(129) ![]()
Substitution into (127) yields:
(130) 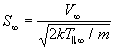
The two parameters M_infinity and S_infinity are easily interchanged and related by:
(131) ![]()
Collisions occurring during the expansion from the nozzle serve to "cool" the seed gas and therefore narrow the width of its velocity distribution (Ref. 59).
For the terminal speed ratio, the following correlation is recommended :
(132) 
where A and B are given in Table 4 and C_6/k=4(epsilon_p/k)sigma_p^6 is given by Table 3. Note that epsilon_p and sigma_p come from pseudopotential calculations and that the cross section (53C_6/kT_o)^1/3 has been written in a form such that it may be replaced by pi sigma^2, a hard-sphere cross section, if it is necessary to estimate S_infinity for expansion from heated sources. The parameters given are from a theoretical model; for monatomic gases, the parameter values derived from experimental fits are also given in Table 4. The results from polyatomic molecules are less reliable, but should be adequate for diatomics, such as nitrogen (N_2), carbon dioxide (CO), or Oxygen (O_2), where vibrational relaxation can be neglected and rotational relaxation occurs far out in the expansion close to where translation relaxation occurs (Ref. 21).
Although the correlation predicts the terminal speed ratio, it can be used to approximate the terminal temperature. Assuming V_parallel,_infinity about V_infinity and combining equations (104) and (130) yields:
(133) 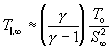
While the previously described correlation can be used to estimate S_infinity or T_parallel,_infinity for polyatomics, these quantities are less reliable than in the case of monoatomics. The difficulty is that two relaxation processes (internal and translational) - that is, two cross sections - are involved and a single, simple correlation cannot be sufficient.
Correlating the perpendicular temperature, T_perpendicular, is as difficult as defining it. T_perpendicular is most directly determined by measuring the lateral spreading of a beam downstream of a skimmer or by careful analysis of the centerline intensity. The difficulty is related to the fact that the temperature is meaningful only when the velocity distribution is gaussian, and this is not true for the perpendicular distribution of velocities far out in the free jet expansion (Ref. 21). As an approximation the expansion is divided by a "quitting surface" into two regimens, a continuum isentropic regimen in which T_parallel=T_perpendicular, followed by a free-molecular, collisionless regimen in which T_parallel remains constant or frozen while T_perpendicular continues to drop. The location of the quitting surface, which is defined as the location where continuum flow ceases and molecular flow starts as shown in Figure 49, can be estimated from the preceding terminal speed ratio correlation. It must be remembered that the quitting surface model is not quantitative. The transition regime is normally very broad. The location of the quitting surface can be estimated by using equation (122) x/d:
(134) 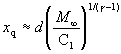
in conjunction with equations (131) and (132).
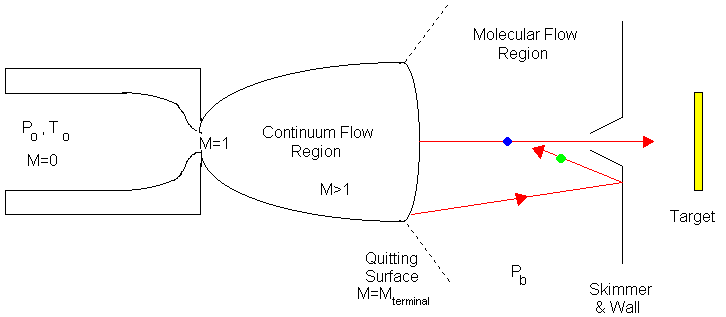
Figure 49: Quitting Surface
Table of Contents