(106) ![]()
and the Mach Number, M, is defined by the ratio of the mass flow speed V to the local speed of sound a:
(107) ![]()
We can write the following equation by combining equations (103), (106), and (107) and eliminating V:
(108) ![]()
By making use of equations (103) and (108) we can write:
(109) ![]()
Further, for an isentropic, ideal gas expansion with gamma = constant we can assume a reversible adiabatic process for which
(110) ![]()
where V in equation (110) is the volume and not the speed. Combining equations (108), (110), and the ideal gas law we get
(111) ![]()
(112) ![]()
Hence, once M is known, all thermodynamic variables can be computed in the free jet. That is the reason why M is used as a universal parameter in characterizing a continuum jet. Again, the assumptions made in deriving these equations are isentropic flow, reversible adiabatic process, ideal gas behavior, constant C_p or gamma, and continuum flow. It is important to note that these equations break down as soon as molecular flow replaces continuum flow.
Considering an isentropic, compressible flow of a single component gas characterized by a molecular weight W and constant specific heat ratio C_p the Mach number M can be obtained as a function of position from the nozzle. The fluid mechanics equations to be solved are the equations for conservation of mass, momentum, and energy. Neglecting viscosity and heat conduction effects, and assuming steady state, a complete set of equations are (Ref. 58):
mass: (113) ![]()
momentum: (114) ![]()
energy: (115) ![]() or (116)
or (116) ![]()
equation of state: (117) ![]()
thermal equation of state: (118) ![]()
Those equations can not be solved analytically for supersonic expansion, but can be solved numerically. Two numerical methods have been used. The first method is the time dependent method. The advantage of the technique is that nonisentropic effects can be treated and it is not limited to supersonic flow. The disadvantage is the great computing time required. The more traditional method is the method of characteristics (MOC). Because this method is simpler and required much less computing time it is usually used. The method is stable, accurate, and fast. The most important group of data for molecular beam researchers are those related to the Mach number values along the centerline, or jet axis, where y = theta = 0, as a function of gamma and position. A set of references using either method is provided in Miller's (Ref. 21) article, as well as an overview on how equations (113) through (118) are solved numerically to obtain the Mach number M as a function of position.
The solution turns out to be independent of source conditions, background pressure P_b, and molecular weight W, and are fitted by:
(119) 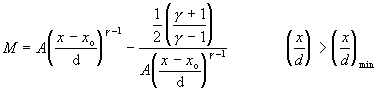
Table 12 contains the necessary constants needed in equation (119) and Figure 47 shows the centerline Mach number dependence on gamma.
Off axis density profiles for axisymmetric flow can be determined using equations (120) and (121). Using these equations one can predict any off-axis property. As one moves away from the centerline x axis in the normal y direction, the density falls approximately as cos^4 theta.
(120) 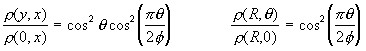
(121) ![]()
Figure 48 shows off-axis contours for a gamma=7/5 axisymmetric expansion. Since constant M means constant properties as shown by equations (108), (111), and (112), these are also contours of constant P, rho, T or collision frequency. Most important, the variation near the centerline is rather flat: M does not vary rapidly with y near the centerline. This equation is based on the fact that far out in the expansion, the streamlines are straight and appear to radiate as in a spherical expansion from a point source at x_o/d, termed virtual source. In molecular beam experiments the far downstream region of the expansion is of most interest. The solid angles involved are always much smaller than unity, therefore only the centerline of the expansion has to be considered.
The following correlation have been used to obtain better fits at small distances x/d<3 in conjunction with Table 13:
(122) 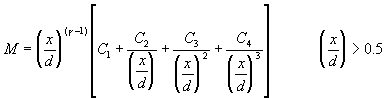
(123) ![]()
Table 13 shows only results for an axisymmetric jet (circular source exit), but data are also available for a planar source (Ref. 21) approximated by a narrow slit of infinite length. As it turns out Mach numbers M achieved by a planar source are smaller.
Just as important as the generality of these results are the limitations caused by the breakdown of continuum flow or nonisentropic effects such as the relaxation of internal energy, nucleation, or chemical reactions. Even without these effects another potential serious approximation is the ideal initial condition on which the MOC solution is based: M about 1 in the plane of the source exit. Pitot tubes studies have shown that the shape and location of the sonic surface depend on source geometry. References to those studies are given in Miller's (Ref. 21) article. While a short converging source does provide a nearly uniform, ideal, planar sonic surface at the exit, a sharp-edged orifice presents a convex sonic surface outside of the orifice with M=1.0 at x/d about 0.25 along the centerline. A long capillary tube appears to provide in the exit plane for an exit Mach number equal to 1.45 implying a transition inside the tube. It was shown though that the free jets are to first order independent of source geometry, especially at x/d>10.
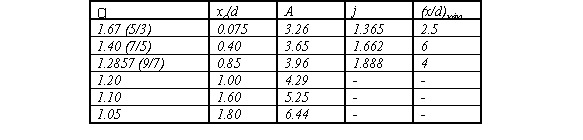
Table 12: Centerline Mach Number for Axisymmetric Flow (Ref. 21)
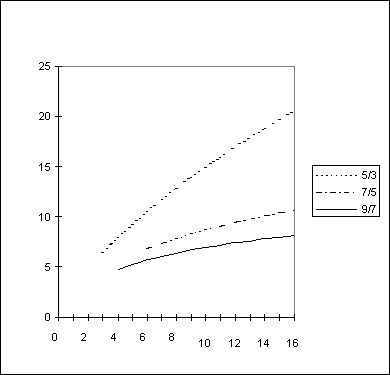
Figure 47: Centerline Mach Number. Dependence on gamma.
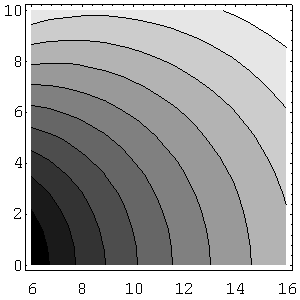
Figure 48: Off-Axis Constant Mach Number Contours y/d versus x/d for gamma=7/5

Table 13: Centerline Mach Number Correlation for Axisymmetric Expansions at Small Distances (Ref. 21)
Table of Contents