(98) ![]()
where h_o is a constant along any streamline and referred to as the total or stagnation enthalpy per unit mass. Since all streamlines originate in the stagnation source, where h=h_o, the constant is the same throughout the expansion. Enthalpy is the relevant quantity instead of internal energy, because the flow is driven by a pressure gradient that accomplishes the flow work, P/rho. Enthalpy decreases and the mean velocity increases as the gas expands and cools. For ideal gases,
(99) ![]()
and, using equation (98), we can write the energy balance relating velocity to temperature as:
(100) 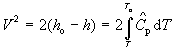
If
![]()
is constant, over the range of interest, T_o to T, then equation (100) becomes:
(101) ![]()
With
(102) 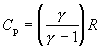
equation (101) becomes:
(103) 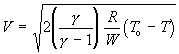
If the gas is cooled substantially during the expansion, T<<T_o, we obtain the maximum or terminal velocity:
(104) 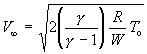
for an ideal gas. For ideal gas mixtures W and C_p are replaced with their molar averages in equation (101):
(105) ![]() and
and 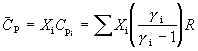
The mean velocity of each specie tends to be the same, in the continuum limit. Therefore each specie in a mixture may acquire energies well above or well below the average, depending on their individual masses. Hence a specie can be accelerated by diluting it in a lighter gas or decelerated by diluting it in a heavier gas. When noncontinuum conditions prevail before the terminal velocity, V_infinity, is reached, velocity slip occurs, as discussed later. It is important to remember that C_p and gamma may not be independent of temperature.
Table of Contents