13.1.2 Appendix - Jet Theory - Structure of a Jet Expansion

Figure 46 shows the complicated structure of a free jet expansion under continuum conditions. All the features shown depend on a continuum fluid mechanics description of the flow, which requires a sufficiently high density and collision frequency to allow for the definition of density, equilibrium temperature, and so on within a reasonable length scale of the apparatus. If these conditions are met shock waves are present in the expansion, which is not the case for our jets as discussed later. Molecular beam researchers complicate the situation further by placing a wall in front of the expansion with a small "skimmer" aperture to extract a centerline "beam", as well as using a collimator for differential pumping, as shown in Figure 2. As discussed later, the situation can be simplified by considering an ideal skimmer placed inside an isentropic region called the zone of silence, or by reducing the background pressure P_b. Reducing the background pressure P_b to low enough values causes the continuum flow to cease before encountering the skimmer or the theoretical shock wave location and therefore the shock wave structure is not present. The latter situation describes our apparatus and operating conditions.

The source shown in Figure 46 has a short converging nozzle. Other nozzle shapes will be treated later and their effect is minor for the properties of interest to us. For this type of nozzle the accelerating flow can be approximated as an isentropic flow, with neglectible viscous and heat conduction effect. The gas starts from a neglectible small velocity, called the stagnation state (P_o, T_o). An imposed pressure difference (P_o-P_b) accelerates, as the area of the nozzle decreases, the gas towards the source exit. The flow may reach sonic speed, but never exceed sonic speed, at the exit, provided the pressure ratio P_o/P_b exceeds a critical value of

(94) 

This equation is obtained from equation (111) discussed later derived from fluid mechanics (Ref. 55) by setting P=P_b and M=1 and is between 1-2 for most gases. Sonic speed is defined as a mean translational velocity equal to the local speed of sound and characterized by a Mach number M equal to 1 since M = V/a where a is the local speed of sound as defined later. If the pressure is less than the critical value G, then the flow will exit subsonically, with exit pressure nearly equal to P_b, without any further expansion. As P_o/P_b increases beyond G, M equals 1 at the source exit or "throat", and the exit pressure becomes independent of P_b and is equal to P_o/G. Since the pressure at the exit now exceeds P_b, the flow is said to be "underexpanded" and a subsequent expansion occurs as the flow attempts to meet the necessary boundary conditions imposed by the background pressure P_b. Molecular beam researchers usually operate under these supersonic conditions.

Supersonic flow has two important characteristics. First, unlike subsonic flows, a supersonic flow increases velocity, or M, as the flow area increases (the "beam" spreads), so that M becomes greater than 1 beyond the exit. Second, a supersonic flow cannot "sense" downstream boundary conditions. This is caused by the fact that the gas moves faster than the speed of sound (M>1) at which information can propagates. Thus, the flow does not "know" about the boundary conditions, yet it must adjust. The resulting dilemma is resolved by the occurrence of shock waves. Shock waves are very thin nonisentropic regions of large density, pressure, temperature, and velocity gradients. Figure 46 shows the occurrence of shock waves. The distance from the nozzle to the shock wave (Mach disk location) can be estimated (Ref. 21) to be

(95) 

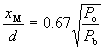
As can be seen the Mach disk location x_M is very insensitive to the gas specie used since there is no gamma dependence. The diameter of the Mach disk can be estimated (Ref. 21) as 0.5x_M +-25%, but the correct value depends on both gamma and (P_o/P_b). The core of the expansion is isentropic and the properties are independent of P_b because the supersonic flow in this region is not aware of any external conditions (hence the term zone of silence).

Most molecular beam researchers operate under conditions where there is no shock wave structure present due to a low background pressure P_b achieved by large pumps used in the region between nozzle and skimmer. The mean free path l_m, according to kinetic theory (Ref. 56), is

(96) 

and can be approximated for air by

(97) 

Assuming a background pressure P_b=1x10^-4 torr, the mean free path would be about 50 cm. The Mach disk location x_M according to equation (95) would be at around 7 cm. The shock wave location would be on the order of the mean free path and therefore a continuum shock wave structure is absent and there is simply a smooth transition from continuum to free molecular flow since P_b is at a low enough value. Therefore the free jet sources discussed here can be visualized as an reversible adiabatic and isentropic expansion into perfect vacuum disregarding any complicated shock wave structures.

The molecular flow is typically affected strongly by the surroundings. First, Beer's law of attenuation by the background gas pressure P_b has to be considered. Second, jet molecules reflected off surfaces placed in front of the expansion play an important role under certain conditions. This effect can be quite large and therefore the skimmer and the wall separating the free jet source chamber from the beam utilization chamber has to be considered as discussed later.

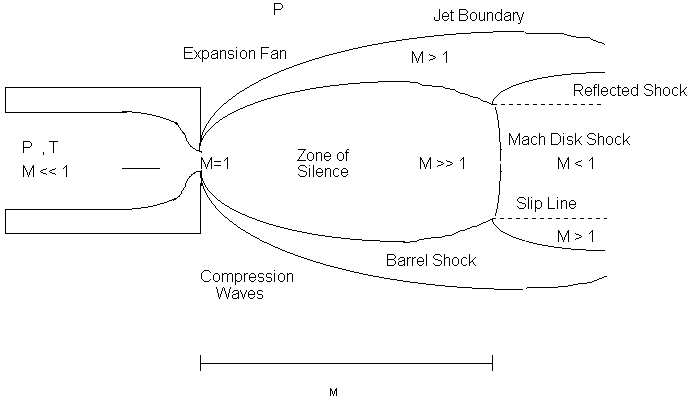
Figure 46: Continuum Jet Expansion

Table of Contents