GaN Growth Investigations - Growth Rate Model for AlN, GaN, and InN

10.5 GaN Growth Investigations - Growth Rate Model for AlN, GaN, and InN

In this section the growth model for the growth rates of AlN, GaN, and InN is further developed and experiments suggested to obtain the necessary constants as well as to verify the model. The model is developed using GaN as an example. Using conservation of flux for the element of interest, in this case Ga, and assuming a fixed NH_3 flux throughout the section unless noted otherwise, the following equation holds:

(75)

Assuming growth at the balance point, having no excess Ga building up, this equation simplifies to:

(76)

The incorporating flux can be expressed in terms of an activation energy as:

(77)

The evaporating flux at the balance point is given by equation (56):

(78)

Substituting equation (77) and (78) into (76) yields:

(79)

Since the substrate temperature range used for growth is very limited, typically between 700°C and 900°C, it is justifiable to express the evaporating flux also in terms of an activation energy:

(80)

Substituting equation (77) and (80) into (76) yields:

(81)

The proper constants for the evaporating flux given by equation (80) have to be determined by curve fitting to equation (78) and are shown in Table 11 for Al, Ga, and In. Figure 37 shows the curve fits, demonstrating the validity of the simplification.

To obtain G^bo_inc and E_inc it was realized that Gamma_inc<<Gamma_evap for all temperatures considered and therefore it is impossible to get accurate data by using equation (76). Instead, we can look at the growth rate G at the balance point which can be written as:

(82)

Note that any negative growth rate due to GaN decomposition is neglected as discussed in an earlier section. Rearranging yields:

(83)

where

(84)

The growth rate above the balance point can be obtained by writing

(85)

as argued earlier, which can be written as:

(86)

where n is the surface Gallium concentration in molecules/cm^2 and n_b is the Gallium surface concentration at the balance point (complete coverage). Rearranging yields:

(87)

Substituting into

(88)

yields

(89)

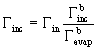
Replacing Gamma^b_evap and Gamma^b_inc with equation (77) and (78) yields:

(90)

Using the simplified equation (80) for the evaporating flux instead of (78) a much simpler expression is obtained:

(91)

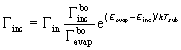
As can be seen from the above equation better growth rates are obtained above the balance point only if E_inc>E_evap. Considering the fact that the growth rate did not change much at different balance points (Superstructure Experiment), equation (83) indicated that E_inc is probably smaller than E_evap. If this proves to be true the balance point gives the highest growth rate for a given substrate temperature, and the balance point at the highest attainable substrate temperature should be used to obtain the maximum possible growth rate with our system.

Different NH_3 fluxes can be included in the model by using a reference NH_3 flux (the fixed flux in the derivations, since G^bo_inc depends on it) and modifying equation (79) to read:

(92)

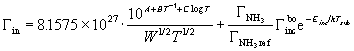
The simplified equation (81) is modified to give:

(93)

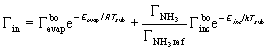
These equations assumes that the incorporation rate increases linearly with NH_3 flux, which makes sense for systems with a very low incorporation rate as N in GaN. Therefore the higher the NH_3 flux at the balance point, the higher the growth rate.

Table 11: Constants for Equation (80) obtained from Curve Fit to Equation (78) shown in Figure 37

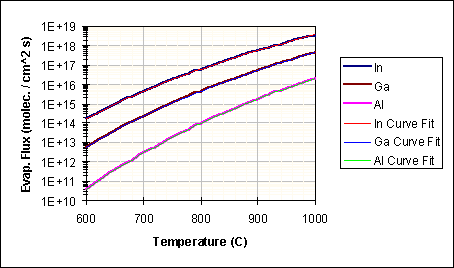
Figure 37: Exponential Curve Fit to Equation (78) using Equation (80)

Table of Contents