![]() (3.1)
(3.1)
Department of Electrical Engineering, University of Minnesota, Minneapolis,
MN 55455
* also, Department of Chemical Engineering and Materials Science, University
of Minnesota, Minneapolis, MN 55455
Surface Review and Letters, 5, 3&4, 1998
PACS 6855, 81.15, 61.14H
For the growth of GaN by MBE using NH3, the kinetics are complicated by (1) the temperature dependence of the dissociation and incorporation of NH3 and (2) the temperature and compositional dependence of the residence times of the reactants on the GaN surface. This means that without knowledge of the microscopic surface processes it is not clear how to set optimum growth parameters. Since the flux and temperature dependencies of the Ga, N, and H surface coverages are not well known, the species that limit the growth can not be easily identified. To monitor these growth processes we have measured structural and compositional changes at the surface with RHEED, and changes in the species leaving the surface with desorption mass spectroscopy (DMS). These two techniques complement each other in determining microscopic processes.
A number of issues related to growth kinetics of GaN must be addressed. Historically, the n-type conductivity commonly exhibited by GaN was attributed to N vacancies [4]. This problem was thought to arise from a kinetic barrier to N incorporation during growth. Results by Lee et. al [5] as well as Jones et. al [6] indicate that the GaN growth rate is strongly temperature dependent, exhibiting a maximum between 750oC and 800oC. The high temperature decrease in growth rate was attributed to Ga desorption at elevated substrate temperature [5,6] as well as to the decomposition of GaN [7]. The common belief at low substrate temperatures is that reduced N incorporation efficiency limits the growth rate [5].
In this paper we will review the growth kinetics on hexagonal films identified as GaN(0001(bar)) [8-10], and show that there are at least two distinct regimes of growth [11-13]. These regimes show different surface morphologies and growth dynamics, primarily due to the surface coverages of Ga and nitrogen, along with hydrogen [14,15]. The main result is that the diffusion length of adsorbed Ga is much smaller under conditions in which the Ga flux limits the rate of growth. However, it is not yet apparent which growth mode is optimal for doping or for growth on strain free surfaces.
In the next section the instrumentation is described, the sample preparation procedures are given, and we show how a GaN(0001(bar)) surface was prepared for this study. Then results of diffraction and mass spectroscopic measurements are presented, which show two growth regimes with different surface dynamics. These growth regimes are then explored in subsequent sections: the details of the diffraction measurements, the nature of the surface processes, and the limits of growth under excess Ga and at high substrate temperatures. From these measurements we develop a simple kinetic model and framework that describes the overall growth.
The sapphire substrate was heated directly by radiation from a high temperature resistive heater made from graphite loops deposited between pyrolytic boron nitride. A thermocouple touched the back of the heater, introducing an offset between the sample surface and thermocouple reading. This offset varied between 50 to 150o, depending upon the growth temperature, as well as from run to run depending on the details of the sample mounting arrangement. This offset was compensated for by determining the surface temperature versus thermocouple reading, as described in detail elsewhere [11] and described in Appendix B.
A 10 keV electron gun was employed for RHEED measurements of the specular intensity without energy filtering. Measurements were made with the electron beam directed along the GaN <1120> azimuth. The diffracted intensity of the specular beam was measured using a phosphor screen and a photo multiplier tube.
Our DMS apparatus is based on a differentially pumped UTI 100 C quadrupole mass-spectrometer mounted on one of the source flanges of the MBE system, permitting the detection of the type and intensity of desorbed species from the sample surface. A similar apparatus has been used by Tsao et al. [16] to study GaAs growth kinetics, and by several workers [6,11,14,17,18] for GaN growth. The solid angle seen by the DMS is limited by the cryoshroud in the growth chamber to subtend only the region around the sample holder. For a few of the measurements to be presented, additional collimation was added in order to limit this region so that only the center of the sample contributed to the desorption signal. This additional collimation reduced the effect of a temperature gradient across the sample as well as the background contribution of surrounding cooler surfaces. Since only a small portion of the sample was subtended, the collimation also reduced the signal to noise ratio. Those measurements performed with the additional collimation are indicated.
Mounting arrangements involving In bonding were found to be unreliable due to evaporation at the high substrate temperatures used in AlN and GaN growth, resulting in cold spots and eventual loss of the sample. Clips that applied even slight pressure induced unwanted stress onto the sample and caused sapphire toCrack during thermal cycling. Instead we used mounts which hold the samples loosely without stress. For 1 inch diameter substrates, this was accomplished by using a retainer ring which screws onto a Mo block. The Mo block has a hole in the center, slightly less than 1 inch, exposing the back of the substrate directly to the heater. Fig. 3 shows the type of sample holder used for square substrates, which has the ability to accommodate any shape and size sample from 3x3 mm to 0.5x0.5 in. via notched interleaving sliders.
C. Nucleation and Buffer Layer
Prior to growth the substrates were outgassed for several hours at 300oC in the preparation chamber of the MBE system, followed by 1 hour at 500oC in the growth chamber. The NH3 leak valve was set to produce a BEP of 1.0x10-5 Torr. Then the substrate temperature was ramped at 100o/min from 500oC to 1000oC for a 15 min surface nitridation. AFM showed that the surface remained atomically smooth after this Al2O3 nitridation.
Experiments were performed by using two types of nucleation layer, AlN and GaN. The 250 Angstrom AlN nucleation layer was grown at 1000oC using an Al flux of 1.2x1014 cm-2s-1 (equivalent to 0.10 ML/s AlN). RHEED showed a transmission pattern during and after AlN growth. The Ga shutter was then opened to provide a flux of 1.1x1015 cm-2s-1 (or 1.0 ML/s GaN) and the sample temperature was ramped down to 800oC at 100o/min. The Al shutter was closed during the ramp below 900oC.
The GaN nucleation layer was grown by repeating a sequence consisting of condensing Ga on the substrate surface at 700oC and subsequent annealing at 800oC under NH3 ten times. This was achieved by ramping the substrate temperature to 700oC, in the presence of an NH3 BEP of 1.0x10-5 Torr. The Ga shutter was then opened at 1.1x1015 cm-2s-1 (or 1.0 ML/s GaN) and the substrate kept at 700oC for about 1 min, during which time the RHEED pattern completely disappeared. The Ga shutter was then closed and the sample ramped to 800oC where it was kept for about 2 min until a RHEED pattern reappeared. This procedure was repeated 10 times, and a transmission RHEED pattern was observed after completion of this nucleation procedure.
Both types of nucleation layer were followed by a 2500 Angstrom GaN buffer layer, deposited at 800oC with a Ga flux of 1.1x1015 cm-2s-1 (or 1.0 ML/s GaN) and an NH3 BEP of 1.0x10-5 Torr. After completion of the buffer layer, RHEED showed a streaky pattern. A (1x1) pattern was observed in the case of using GaN nucleation, while a very weak (2x2) reconstruction was typically observed using AlN nucleation. For this study, films grown with an AlN nucleation layer were found to be predominantly GaN(0001(bar)) oriented featuring inversion domains, while the GaN initiation layer resulted in unipolar GaN(0001(bar)) surfaces. [8]
The two main surface morphologies observed in the MBE growth of GaN(0001(bar)) on sapphire are illustrated by RHEED and AFM data in Fig. 4. Both films were grown under similar conditions but with very different Ga fluxes. Both GaN films are 0.8 um thick and were grown using an AlN nucleation layer, which typically produces some inversion domains [8]. Growth rates were 0.5 um/h with an NH3 BEP of 1.0x10-5 Torr at a substrate temperature of 800oC. Fig. 4a and c show RHEED and AFM data for a Ga flux of 1.1x1015 cm-2s-1 (or 1.0 ML/s GaN) while Fig. 4b and d show data for a sample grown with a Ga flux of 6x1014 cm-2s-1 (or 0.5 ML/s GaN). AFM reveals that the film grown with a higher Ga flux is locally smoother, featuring atomic steps with 50 nm terraces, than the one grown with a lower Ga flux. Similar to what is shown by the AFM data, the RHEED pattern shows a well defined specular beam with long streaks, indicative of two-dimensional layers with random atomic steps. The surface exhibited a very weak (2x2) reconstruction. By contrast, the film grown at a lower Ga flux is much rougher and faceted. Consistent with these AFM results, the RHEED pattern shows transmission-like features that do not move as the incident electron angle is changed. Similar results are obtained on films with single-domain GaN, grown with GaN nucleation layers, and on bulk GaN(0001(bar)), also free of inversion domains. These two morphologies are seen in the following subsections toCorrespond to distinct growth regimes.
The growth dynamics are also very different under these two Ga:NH3 flux ratios. Two examples of the evolution of the surface structure, as measured by the specular RHEED intensity versus time, are shown in Fig. 5 and Fig. 6. In Fig. 5 we plot the intensity of the specular RHEED beam vs time for a sample held at 670oC for a low Ga:NH3 flux ratio, while Fig. 6 shows a similar plot for a sample held at 780oC at a high Ga:NH3 flux ratio. These are distinctly different behaviors, with one showing island nucleation and the other suggesting step flow. With DMS we will explore the rate limiting reactions as well as the composition and reactivity of the surfaces corresponding to these growth conditions. We will show that island nucleation observed in these RHEED data correspond to Ga limited growth while step flow corresponds to NH3 limited growth.
If the desorbed Ga flux is small, we instead use the desorbed H2 signal. Fig. 7b shows that H2 is released during growth using NH3. This figure is a plot of the H2 signal vs time with the sample under constant NH3 flux, while opening and closing the Ga shutter. Under the assumption that this increased H2 desorption is attributed to the forward reaction
![]() (3.1)
(3.1)
we can obtain relative growth rates. Measurement of the H2 DMS signal is especially useful when the Ga signal is below the detection limit of the DMS. The H2 signal intensity is larger because lower mass ions have a larger transmission through the mass spectrometer. A disadvantage of this technique is that absolute growth rates cannot be determined as easily. Nonetheless in combination with measurement of the Ga signal, growth rates can be determined over a wide range of conditions. These DMS measurements that identify the rate-limiting fluxes are particularly important since RHEED is not able to measure growth rates under conditions of step-flow growth.
Applying the above methods, Fig. 8 shows the GaN growth rate vs NH3 flux at a fixed Ga flux and substrate temperature. These data represent a series of in situ measurements on the same sample, with 15 min of growth between data points under conditions of the point to be measured. The H2 signal is proportional to the Ga data, indicating that using the H2 signal is a valid method of obtaining relative growth rates. Growth rates calculated from the Ga signal agreed well with stylus and RBS measurements. From this figure a number of observations can be made: At low NH3 fluxes the growth rate is approximately a linear function of the NH3 flux, suggesting that a fixed fraction of the available NH3 contributes to GaN formation. The deviation from linearity will be discussed later in terms of a proposed growth model. At high NH3 fluxes no Ga desorption is measured. Hence the growth rate is a constant with unity Ga incorporation, within an uncertainty of less than 15%. The crossover between those two regimes is relatively abrupt, allowing the identification of at least two growth regimes: when there is excess Ga, the growth rate is limited by the NH3 flux; when there is excess NH3, the rate is limited by the Ga flux.
The crossover can also be seen by measuring the growth rate as a function of Ga flux, at a fixed NH3 flux and substrate temperature. The results are shown in Fig. 9. From this figure we can make the following conclusions about the MBE growth of GaN(0001(bar)): At low Ga fluxes the growth is Ga limited, as was observed above. At higher Ga fluxes a desorbed Ga signal was measured, indicating that not all Ga was incorporated and that there is insufficient NH3. At these fluxes growth is thus NH3 limited. Further, the growth rate decreased with increasing Ga flux, going towards zero. In Sec. III E 1 we will show that the flux at which the growth ceased corresponds to the condensation condition for this substrate temperature. This can also be seen in Fig. 10 where the growth rate is plotted as a function of substrate temperature in the NH3-limited regime.
C. RHEED Measurements
Further, these intensity oscillations are not characteristic of a narrow growth front. Instead, continued growth eventually led to a transmission RHEED pattern. And, except perhaps at very high temperatures, the intensity does not recover upon closing the Ga shutter. In the case of other III-V semiconductor growth, such as GaAs(100), growth interruption at the growth temperature is sufficient to prepare a surface sufficiently smooth to subsequently observe intensity oscillations. But here, in order to repeat a series of intensity oscillations, an anneal to as high as 800oC was necessary. Alternatively a smoothing procedure involving growth in the NH3-limited regime was helpful. Growth in the NH3-limited regime, as described below, usually resulted in subsequently stronger oscillations than just annealing.
The process for smoothening by overgrowth starts by depositing approximately 100 Angstrom of GaN in the NH3-limited regime. Typical conditions are a substrate temperature of 800oC, a Ga flux of 1.1x1015 cm-2s-1 (or 1.0 ML/s GaN), and an NH3 BEP of 1.0x10-5 Torr. After this smoothening step strong oscillations could again be observed. It should be noted that we observed these strong oscillations only when using a GaN nucleation layer, while in the case of an AlN nucleation layer oscillations were not observed or at best were exceedingly weak.
We also obtained damped AlN RHEED intensity oscillations by growing on GaN, as shown in Fig. 11, using similar conditions and surface preparation procedures as for GaN on GaN. These oscillations correlate roughly to monolayer growth with unity Al incorporation. The GaN film was prepared by the previously described overgrowth method in the NH3-limited regime. Then the substrate temperature was lowered to 670oC and the Al shutter opened at a flux of approximately 0.2 ML/s. The main requirement was preparation of a sufficiently smooth surface and growth under high NH3 flux.
GaN RHEED intensity oscillations cannot be used directly to measure growth rate, as shown in Fig. 12. Here the frequency from data like those measured in Fig. 5 are plotted as a function of Ga flux at two different NH3 fluxes. Contrary to previous suggestions [20,19], the period of these oscillations does not correspond exactly to monolayer (half a conventional unit cell) layer deposition. Note that the Ga flux was calibrated from GaAs intensity oscillations measured in the same growth chamber. The slope of the curve is about 0.9 for the fluxes investigated, and there is an offset of up to -0.08 ML/s at zero Ga flux. This offset depends on the NH3 flux, increasing with increasing NH3 flux.
The temperature dependence of the oscillations at different Ga fluxes is shown in Fig. 13. For these three fluxes no oscillations were observed outside the temperature range covered, and the strongest and longest lasting oscillations were observed at the lowest temperature of each curve. Below this temperature, we noticed that continued growth will not result in a transmission RHEED pattern, but a pattern that indicated amorphous growth, representing the low temperature limit of single crystal GaN growth in the Ga-limited regime. At high substrate temperatures the oscillation frequency decreases, and the activation energy of this decrease was found to be 1.2 eV. Other samples with miscuts ranging from 0 to +-0.3o off the c-axis, including stress-free bulk GaN samples [8], gave similar results. This reduction is not due to Ga desorbing from the GaN surface, as verified by DMS earlier under similar conditions. We propose that this reduction in RHEED oscillation frequency is due to Ga atoms diffusing to step edges, participating in step flow growth, and therefore not contributing to the oscillations.
Above about 850oC, with excess NH3, intensity oscillations were not observed. At these temperatures, the streaks in the initial RHEED pattern from a smooth surface transform into a 3D transmission pattern of spots, and the corresponding RHEED intensity shows a slow decrease. This transition to 3D was somewhat slower as the NH3 flux was reduced. This is much different from the case of NH3-limited growth, showing a rapid initial decrease upon opening of the Ga shutter, as presented earlier in Fig. 6. The behavior at high temperature in the Ga limited regime is likely due to the increase in the sublimation of GaN along with the reduction in the rate at which Ga incorporates into islands.
The key RHEED intensity behavior is shown in Fig. 6, where the specular RHEED intensity is plotted from a GaN surface during and after Ga exposure at three different substrate temperatures. The Ga shutter is opened at time t1 and later closed at t4. The incident Ga and NH3 fluxes were the same for all three curves. The starting RHEED intensity depends only on whether there has been sufficient initial NH3 exposure. We used about 100 Langmuirs, to completely nitride the surface as discussed in Sec. III D (Note that 1 Langmuir equals equals an exposure sufficient to adsorb 1 ML with unity incorporation.). This nitridation is relatively independent of typical growth temperatures. Three distinct behaviors are observed: Curve (a), measured at Ts=800oC, shows between t1 and t3 an initial rapid decrease to a value that is relatively constant, and then at time t4 a rapid recovery. Curve (b), measured at a temperature 5oC lower, shows a similar but larger decrease to a constant value, as well as a rapid recovery. And curve (c), reduced by an additional 5oC, shows a similar initial behavior but then a slower steady decrease, followed by a two stage recovery having a slow and fast component. For the high and medium temperature case, the magnitude of this decrease is a function of growth parameters, less at higher substrate temperatures, higher NH3 fluxes, and lower Ga fluxes. For the low temperature case, the magnitude of the initial rapid decrease is independent of temperature. However the subsequent slower decrease becomes steeper with lower temperatures. After closing the Ga shutter the time required for the first stage of the two stage recovery increases with lower temperatures.
The transition between curve (b) and (c) is very abrupt -- a temperature change of a few degrees is sufficient for its observation. It was found that this transition is independent of NH3 flux in the excess Ga regime (under excess NH3 it is completely absent). We interpret the transition between curve (b) and (c) to correspond to the temperature, Tc, at which Ga condenses on the GaN surface. Sec. IV A we will compare the RHEED data with DMS measurements, connecting the transition with the amount of adsorbed Ga.
First, a surface was prepared by exposure of a GaN(0001(bar)) film to an NH3 flux in the absence of Ga. After a 100 Langmuir exposure, the specular RHEED intensity had reached a maximum value. This nitrided surface is a stable termination since it does not change after the NH3 flux is removed and serves as the starting surface for the measurements in Fig. 14.
Preparation of a GaN(0001(bar)) surface with a Ga termination is illustrated in Fig. 14. A substrate temperature above that for Ga condensation was chosen (cf. Sec. III E 1). A nitrided surface was then exposed to a Ga flux in the absence of NH3 while monitoring the specular diffracted intensity as well as the desorbing Ga. After opening the shutter at t1, the RHEED intensity decreased to a steady state value at t3, after going through a change in slope at t2. The time to reach this steady state depended on the Ga flux. Since this is a steady state condition, the Ga desorption flux is equal to the incident flux. The Ga shutter was then closed at t4, at which time the RHEED intensity increased until it reached at t6 an intensity marked level 2, and the DMS signal simultaneously decreased to a background. The final RHEED intensity was independent of the steady state Ga coverage that was achieved during deposition, when the RHEED intensity was below level 2. The DMS shows Ga desorbing, beyond t4, which must be weakly bound compared to any Ga remaining at t6. This last surface is stable in the absence of a Ga or NH3 flux. Our interpretation of this data is that this surface consists of a strongly bound Ga termination layer on GaN(0001(bar)).
If the surface is subsequently reacted with NH3 , the behavior seen in Fig. 6 would again be obtained and the RHEED intensity rises to the nitrided value of level 1. These observations indicate that there are at least two stable surface terminations possible on GaN(0001(bar)) -- one is reached after the GaN surface is exposed to an NH3 flux in the absence of Ga (level 1), and the other is obtained after Ga exposure, followed by an anneal in the absence of both NH3 and Ga (level 2).
Knowing how to prepare these two surface terminations on GaN(0001(bar)), we looked for the reconstructions reported by Smith et al. [9], who used a hydrogen free, RF plasma as a nitrogen source. We found that in order to obtain the same reconstructions, the Ga termination had to be prepared first. Then the sample temperature was lowered to 400oC. After deposition of additional Ga, the substrate temperature was lowered to below 300oC and all of the reconstructions reported by Smith were observed, depending on the coverage of weakly bound Ga deposited. This suggests that H plays no role in the symmetry of partial Ga coverages on the Ga terminated, GaN(0001(bar)) surface.
The transient response of the specular RHEED intensity as well as the response of the desorbed Ga and H2 fluxes to a step-function of incident Ga on the GaN surface are shown in Fig. 15. These data were measured after growth had been stopped and the surface was nitrided. Then the background NH3 pressure was reduced to 10-9 Torr while maintaining a constant substrate temperature of 760oC.
A number of important features are observed in Fig. 15 after opening the Ga shutter at a substrate temperature above Ga condensation. The initial shoulder in the curve corresponds to an initially low Ga desorption flux. This indicates that Ga adsorbs in a strongly bound site until the available sites are saturated. We also see a H2 pulse that is a by-product of this adsorption process, indicating that this surface contains H [14] After deposition of roughly one monolayer, the Ga desorption increases and the H2 desorption decreases, indicating the presence of a second, weakly bound state. These results are consistent with the data showing two adsorption sites presented in Sec. III D 1. After the initial Ga pulse, we close the Ga shutter and allow the weakly bound Ga to desorb from the surface. Subsequent exposure to incident Ga results in only the higher Ga desorption flux, with no detectable change in the H2 desorption. This indicates that the hydrogen left in the nitridation process has been depleted. The hydrogen released required approximately one ML of incident Ga, deduced from the area under the desorbed Ga curve. Further, no additional Ga is adsorbed into the strongly bound sites, confirming that those sites are stable with time in the absence of any fluxes. We can again prepare a surface that would adsorb Ga in the strongly bound sites by exposing the sample to NH3.
To quantify the Ga adsorption we measured the RHEED intensity and plotted its derivative for different growth conditions. Fig. 16 shows a measurement which was performed under NH3 exposure while opening the Ga shutter. The derivative clearly reveals that two slope maxima occur during the initial transient RHEED decrease. Quantitative information can be extracted from this RHEED intensity variation by definition of a time interval, Delta t, as indicated in Fig. 16. We find that the time dependence of the transient Ga and H2 desorption track variations in the RHEED intensity, exhibiting a change in slope. Based on this observation we conclude that Delta t gives an estimate of the time required for saturation of the strongly bound Ga sites.
The dependence of Delta t on both NH3 and Ga flux is shown in Figure Fig. 17, which shows 1/Delta t versus NH3 BEP for three different Ga fluxes. We see that 1/Delta t increases for increasing Ga flux, but that it decreases as the incident NH3 flux is increased. We note that the intercept on the 1/Delta t axis is nearly equal to the incident Ga flux for all three curves, again suggesting that 1 ML of Ga can be adsorbed in strongly bound sites on a nitrided surface. The decrease in 1/Delta t with increasing NH3 pressure indicates that the physical process responsible for these transients is slowed by increasing the amount of incident NH3.
A simple first order estimate of the time required for a termination change from a nitrided to a surface with strongly bound Ga sites can account for this behavior. In this model we assume the Ga diffusion length is large so every incident Ga atom will react with the nitrided surface. We wish to estimate the time required for the entire surface to become Ga terminated. We neglect the small desorption of Ga from the strongly bound sites observed in Fig. 15. The time derivative of the N-H surface coverage, thetaN, is given by the difference between the incident fluxes
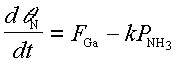 (3.2)
(3.2)
where FGa is the incident Ga flux in ML/s, and kPNH3 is the active N flux in ML/s as supplied by the NH3, with k being the system dependent conversion factor between measured NH3 BEP and active N flux. Solving Eq. (3.2) subject to the initial condition thetaN = 1 at t = 0 we find that
![]() (3.3)
(3.3)
and from this we see that thetaN = 0 when t = 1/(FGa - kPNH3), which is the time required to change all of the surface sites from N(H) terminated to Ga terminated. Consistent with this simple picture of the surface kinetics is the observation that the linear curve fits shown in Fig. 17 intercept with the 1/Delta t axis close to the incident Ga flux, as expected from Eq. (3.3).
The data in Fig. 19 point to a crucial aspect of growth under conditions of excess Ga. If we take the H2 signal to be proportional to the GaN growth rate, these data indicate that the growth rate is enhanced in this NH3-limited regime just after opening and closing the Ga shutter. We have shown in III D 1 and Sec. III D 2 that Ga adsorbs in two adsorption sites, strongly bound and weakly bound. After closing the Ga shutter the weakly adsorbed Ga either desorbs or is consumed by active N sites. Similarly, just after initiating the Ga flux, Ga first adsorbs into strongly bound sites, and then into weakly bound sites. The enhancement occurs during those times when the coverage of weakly adsorbed Ga is lower than that at steady state during growth. This behavior suggests that the presence of weakly bound Ga reduces the growth rate. In other words, this suggests that when excess Ga atoms are in the lattice sites deduced by Smith [9], the growth rate is reduced from its maximum value. We will include this in a first order model [14] in Sec. IV B.
This same adsorption behavior in this excess Ga regime was also seen in the RHEED data of Fig. 6, where we interpreted the transition between curve (b) and (c) to correspond to the temperature, Tc, at which Ga condenses. This behavior was not observed in the Ga-limited regime. Instead, RHEED intensity oscillations, as shown in Fig. 5, were recorded at low temperatures, their frequency indicating near unity Ga incorporation. These results indicate that the GaN growth kinetics in those two regimes differ significantly. We identify the abrupt transition temperature, between growth and no growth, as the temperature at which multilayers of Ga begin to condense on the surface.
To correlate RHEED and DMS measurements in terms of Ga condensation and surface termination, we compare in Fig. 21 measurements of the desorbed Ga to the corresponding RHEED intensity vs time, at a temperature below Tc at which Ga condenses on the surface. To improve the signal to noise ratio we did not use collimation for this set of DMS measurements and therefore the DMS averages over the entire surface of the 1 inch sample. The RHEED measurement, on the other hand, is more localized, and by moving the beam across the surface we determined that there was an approximately 30o temperature gradient across the sample surface. After opening the Ga shutter at t1, the decrease in the RHEED intensity parallels an increase in the Ga DMS signal to a steady state value at t3. There is a slight decrease in the RHEED intensity after t3 due to increased attenuation of the signal originating from ordered regions. By contrast, the Ga DMS signal is constant after t3. This is consistent ifthe desorption energies from successive layers are approximately equal. The magnitude of this desorbed Ga is independent of temperature above Tc and then decreases below Tc due to condensation.
The recovery behavior of the two signals after the Ga source is shuttered are alsoCorrelated to an extent -- the DMS indicates that the increase in the diffracted intensity can be associated with a decrease in the amount of adsorbed Ga and not just to a coalescence of surface adatoms that reduces the step density. The correlation is not exact, however. After the Ga source is shuttered at t4 the RHEED intensity increases slightly until, at t5, there is a rapid increase. The DMS signal remains constant during this time and then decreases to a background. Difference in recovery rates would be expected if regions on the sample surface at lower temperature, where there is a larger amount of condensed Ga to desorb, alsoContribute to the DMS signal. Thus the condensation is seen in both the RHEED and DMS data, though regions sampled can be quite different.
Determination of the GaN decomposition rate was accomplished by monitoring both Ga and molecular nitrogen signals while varying the substrate temperature. The Ga signal coming from the GaN sample, as detected by the DMS, was calibrated previously in terms of absolute flux. This was achieved by exposing the GaN sample with a known Ga flux above the condensation temperature, at which the incident flux equals the desorbing flux. The incident flux was known from the measurement of RHEED intensity oscillations during growth of GaAs(001) in a separate experiment.
Quantification of the N2 flux desorbing from the substrate was not possible by direct means. However, a useful comparison between N2 and Ga signals can be obtained assuming that sublimation is congruent. In this case, the N2 flux leaving the substrate is related to the Ga flux leaving the substrate via the relation
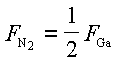 (3.4)
(3.4)
Hence, to within a scale factor that depends on the sensitivity of the mass spectrometer, the two signals should equal. In Fig. 22 we show a plot of 1/2 FN2 and FGa versus substrate temperature resulting from GaN decomposition. The scale factor used to obtain the absolute N2 flux is based on the assumption of congruent sublimation. The assumption is justified by the fact that the slope of the twoCurves are the same to within the experimental error. We see that the data presented here are consistent with previous measurements [22], and also that these results extend the temperature range of available experimental data. The activation energy of GaN decomposition was therefore verified to be 3.4 eV in the experimental range covered. It was found that the GaN decomposition rate reduces in the presence of Ga, consistent with the law of mass action, published elsewhere in detail [23]. The exact dependence of GaN decomposition in the two growth regimes, as a function of both Ga and NH3 fluxes, still has to be investigated and we expect the results to follow the law of mass action. The main point is that at growth temperatures above 800oC the growth rate can be reduced significantly due to GaN decomposition, which cannot be neglected in an overall growth model.
IV. Discussion
The DMS and RHEED data presented in Sec. III can be understood by considering the adsorption of Ga onto an otherwise inert surface in the absence of NH3. Examine two limits: First, at sufficiently high temperature, an incident Ga flux will produce a steady state Ga coverage that depends on the incident Ga flux and the Ga residence time. In this steady state, the total amount of adsorbed Ga is constant so that the incident flux must equal the desorbing flux. Second, if the substrate temperature is decreased sufficiently, there will be a temperature below which Ga condenses on the surface forming multilayers and/or droplets. Below this temperature the system is not in steady state since the incident flux exceeds the desorbing flux, and Ga is adsorbed continuously. The transition from steady state to condensation is sharp and can be determined by measuring the temperature at which the desorbed Ga flux begins to decrease. For a given incident Ga flux, this transition corresponds to a unique surface temperature well described by equilibrium vapor pressure data.
The picture that emerges is illustrated in Fig. 23 where weakly bound Ga adsorbed on Ga terminated GaN(0001(bar)) is shown. In this situation, if there were no NH3 or Ga flux present, the weakly bound Ga desorbs, leaving the strongly bound Ga to make up the Ga terminated GaN(0001(bar)) surface. If now an NH3 flux is provided, the strongly bound Ga of the Ga terminated surface would react resulting in a nitrided surface. If then a Ga flux is provided to this nitrided surface, in the absence of NH3, the Ga would react with the nitrided surface causing hydrogen to desorb. After the nitrogen is consumed by strongly binding Ga, a surface coverage of weakly bound Ga will built up. If the substrate temperature is above the condensation temperature the weakly bound Ga, likely less than a monolayer, will reach steady state, as shown in Fig. 23a. If the substrate temperature is below the condensation temperature for that incident Ga flux, Ga multilayers and/or droplets will form, illustrated in Fig. 23c. The crossover between steady state coverage of weakly adsorbed Ga and condensation is shown in Fig. 23b. Once the Ga flux is stopped, any weakly bound Ga will again desorb to eventually expose the strongly bound Ga terminated surface.
During growth the steady state coverage of weakly adsorbed Ga is maintained by the incident Ga minus the desorbing Ga and Ga forming GaN. We will present a model in Sec. IV B in which the strongly bound Ga contributes to growth, whereas the weakly bound Ga acts to inhibit growth by blocking these strongly bound Ga sites. The effect of weakly adsorbed Ga on growth rate can only be observed in the NH3-limited regime, while in the Ga-limited regime near unity incorporation of Ga is obtained, as discussed later in Sec. IV C.
We assume that NH3 reacts only with strongly bound Ga, and that the excess Ga in the weakly bound site reduces the growth rate by blocking the underlying reactive Ga sites. Further motivation for such a growth mechanism can be found in the work of Liu and Stevenson [25], who found that the coexistence of Ga and GaN enhanced the decomposition of NH3 relative to Ga alone.
We let the growth rate be proportional to the fraction of strongly bound Ga sites that are exposed to the incident NH3 , (1 - sigmaGa). DMS measurements of the H2 flux showed that the NH3 reactivity does not depend on substrate temperature over the range (700oC-820oC), and we therefore let the active N flux, FN, be independent of substrate temperature. We wish to determine the steady-state growth rate when the incident Ga flux exceeds the active N flux, FGa > FN. The time derivative of the Ga coverage is given by
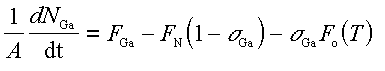 ,
(4.1)
,
(4.1)
where the growth rate is FN(1 - sigmaGa), and NGa is the number of weakly bound Ga atoms on the substrate surface of area A. Solving Eq. 4.1 for sigmaGa at steady-state gives the growth rate
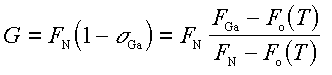 .
(4.2)
.
(4.2)
The result of this model is shown as a solid line in Fig. 9. As stated earlier, we estimate the desorption term Fo(Tsub) from the equilibrium vapor pressure of Ga over liquid Ga [26]. We see from Fig. 9 that the growth rate as extracted from the Ga data is in reasonable agreement with the steady-state solution given in Eq. 4.2. The only fitting parameter used was FN, which is equated to the known Ga flux for which the growth rate is maximum. The main point to be extracted from this discussion is that weakly adsorbed Ga reduces the formation rate of GaN. The model predicts further that the growth ceases completely when FGa = Fo(Tsub), where sigmaGa = 1. This is completely consistent with the results of Sec. III E 1, where we found that the onset of Ga condensation is independent of NH3 flux in the NH3-limited regime. Eq. 4.2 was also applied to Fig. 8 predicting a deviation from a linear increase in growth rate as a function of NH3 flux in the NH3-limited regime. This deviation from linearity decreases with increasing substrate temperature due to a reduction in the coverage of weakly adsorbed Ga.
This result shows that we can use substrate temperature to control the coverage of weakly adsorbed Ga. For example we can increase the growth rate by increasing the substrate temperature, in effect reducing the steady state surface coverage of weakly adsorbed Ga. This is seen in Fig. 10 where the GaN growth rate is plotted as a function of substrate temperature at a fixed Ga and NH3 flux. The result is counter to the notion that decreased Ga residence times at higher temperature lead to decreased growth rates [18] as discussed below. We attribute the drop in growth rate at high temperatures to GaN decomposition competing with growth. This conclusion is motivated by comparing the data to the proposed growth rate model, Eq. 4.2. Two solid curves are shown in Fig. 10, the top one showing the growth rate as given by Eq. 4.2, while the bottom one is given by Eq. 4.2 minus the GaN decomposition rate in the absence of any fluxes. The measured data fall between those twoCurves, suggesting that GaN decomposition is responsible for the growth rate reduction. Further, during growth, GaN decomposition is suppressed compared to the decomposition measured in the absence of any fluxes [23].
A similar drop in growth rate was observed by Guha et al [18] at a much lower substrate temperature, and they attributed this reduction to the decrease in residence time of the incident Ga on the GaN surface. However, their data were apparently taken in the Ga-limited regime, but close to the NH3-limited regime, at a Ga flux of 0.6 ML/s and an active N flux of 0.8 ML/s. The substrate temperature ranged from 720oC to 840oC, and the growth rate decreased from 0.5 ML/s at 720oC to zero at approximately 760oC. Those results are in sharp contrast to ours which were obtained at what should have been very similar growth conditions. Fig. 9 indicates that at a Ga flux of 0.6 ML/s and an active N flux of only 0.5 ML/s, at a substrate temperature of 785oC, all of the available Ga incorporates within the measurement error of less than 0.1 ML/s. Even though our data were taken at a substrate temperature 25o higher, as well as at a lower active N flux, they disagree significantly with Guha's results. Possible differences include errors in substrate temperature determination as well as differences in growth kinetics between NH3 and RF nitrogen sources.
Assuming that the RHEED intensity oscillations indicate the true growth rate, we are losing some of the incident Ga either by desorption, scattering, or accumulation. In the case of desorption we expect that by increasing the NH3 flux we can increase the probability of incident Ga to combine with Nitrogen sites, effectively increasing the slope of the curve. On the other hand, the mean free path of the Ga atoms between the source and the sample shortens at the high NH3 pressures used, which should result in a decrease in slope. In either case the constant offset observed is not expected. When increasing the NH3 flux this offset increased, but the slope of the curve did not change as we might expect. No evidence of Ga accumulation was observed either to explain the behavior.
If we consider the case that the RHEED intensity oscillations do not indicate the true growth rate, we conclude that we are losing some Ga that does not take part in island nucleation. Possibilities might be the migration of Ga atoms to step edges participating in step flow, or the migration to defects on the GaN surface. It becomes evident that a more detailed study is needed to resolve the issue, keeping in mind that several processes combined might be responsible for the observed behavior.
Finally we should mention that part of the differences obtained between films grown under NH3 limited conditions and those under Ga limited conditions might be due to the presence of inversion domains. For example, Romano and Myers [27] have recently examined growth on mixed polarity films, using plasma sources for N, and showed that one polarity grows faster than the other under excess N conditions, and that more balanced growth rates are obtained under excess Ga. This resulted in smoother films under excess Ga compared to excess N. We found however, that even by growing on bulk unipolar GaN(0001(bar)) surfaces, films showed the 2D and 3D growth regimes. Further, these latter films could be annealed at 800oC, as indicated by a reduction in the intensity of the 3-D transmission RHEED features. This suggests that changes in surface diffusion play a dominant role.
For example, if FN and a substrate temperature corresponding to point (a) were chosen, then the growth would be Ga limited (excess NH3 ) and the growth would be 3D. At somewhat higher NH3 fluxes, RHEED intensity oscillations would be observed on initially smooth surfaces. Similarly, at point (b, the growth would be Ga-limited and 3D, though at these substrate temperatures, the decomposition of GaN becomes significant and reduces the growth rate. In this Ga-limited mode RHEED intensity oscillations are observed, and the observed decrease in oscillation frequency indicates that Ga diffusion can be increased by raising the substrate temperature.
Alternatively, if FN is less than FGa then the growth is NH3-limited (excess Ga) and is described by the data below the horizontal solid line corresponding to the incident Ga flux. The key temperature value corresponds to the intersection of F = Fo(T) and F = FGa. This is the condensation temperature, Tc, and is indicated by the vertical dashed line since it is unchanged for all lower NH3 fluxes at this incident FGa. For any NH3 flux in the shaded region to the right of Tc, for example at point (h), Ga will condense on the surface since the incident Ga flux, FGa, is greater than the flux that would desorb from liquid Ga. There is no GaN growth in this regime. Our results do not show a reduction in desorbed Ga flux in this region when NH3 is introduced.
In the 2D regime, at temperatures higher than Tc and under excess Ga, growth is possible since multilayers of Ga that would otherwise block growth do not form. In this regime, surface diffusion is evidently high and RHEED oscillations are not observed. We assume that this corresponds to step-flow growth. The arrows in this region summarize the results of much of the data presented in Sec. III and the model of Sec. IV B. Under these conditions the GaN(0001(bar)) surface is terminated by a layer of strongly bound Ga that reacts with NH3. However, additional weakly adsorbed Ga blocks growth and reduces the growth rate. The change in growth rate vs NH3 flux, shown in Fig. 8, corresponds to the arrow from (c)-(e). Along this line the main effect is that the growth rate is limited by the arrival of nitrogen and so increases approximately linearly with NH3 flux. However it does not increase linearly with unity slope since initially there is some fraction of a ML of weakly adsorbed Ga on the surface that blocks growth. As the NH3 flux is increased, the coverage of weakly adsorbed Ga is reduced and hence the fraction of the NH3 that can be incorporated increases. Similarly, the arrow from point (e) to (f) is illustrated by the data in Fig. 10. At point (e) there is a fraction of a ML of weakly adsorbed Ga on the surface that blocks reaction with the strongly adsorbed Ga. As the substrate temperature is increased, at a fixed Ga and NH3 flux, the coverage of weakly adsorbed Ga decreases and the growth rate increases. As point (f) is reached, the decomposition of GaN becomes important and there is a reduction in growth rate. If the substrate temperature were increased past the decomposition line to point (g), there would be no net growth and the decomposition of GaN would dominate.
We consider deposition onto a surface at a temperature above which Ga condenses. A fraction of the incident Ga incorporates as GaN, and the remainder supplies a steady-state Ga surface coverage which desorbs at the same rate at which it is supplied. Without any NH3 flux all the incident Ga desorbs. We assume that an NH3 flux does not affect the angular distribution of the desorbed Ga flux. In order to obtain the incorporating flux we measure the difference between these two Ga desorption fluxes.
An examples of the Ga desorption signal with and without NH3 is shown in Fig. 7a taken without collimation to improve the signal to noise ratio. Here we measure the change in the desorbed Ga signal when the Ga flux is interrupted since it is somewhat easier to be certain that steady state signals are measured. With NH3 impinging on the surface GaN is grown until steady state conditions are obtained. The Ga flux is then interrupted and the DMS signal quickly decreases to a constant background level. We take the drop in the measured mass spectrometer current, Delta Igrowth, to be proportional to the Ga flux leaving the sample surface. Similarly, without NH3, there is a drop in the Ga reference signal, Delta Iref, that is proportional to the incident Ga flux. The growth rate is then computed from
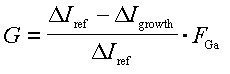 ,
(A1)
,
(A1)
using FGa as measured by GaAs RHEED intensity oscillations and implicitly taking into account the proportionality factor between the measured mass spectrometer current and the desorption flux. Note that at substrate temperatures greater than about 800oC the decomposition of GaN, not included in Eq. A1, must also be considered.
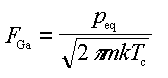 ,
(B1)
,
(B1)
where peq is usually tabulated as [26]:
![]() (B2)
(B2)
with p given in units of atm., A = 6.754, B = -13984, and C = -0.3413. Here Gammain is the incident Ga flux and T = Tc.
Alternatively, both the incident and desorbing fluxes can be expressed more symmetrically by measuring the incident flux in GaN monolayers per second, 1/taui, and by fitting the flux desorbing from the surface in the right side of Eq. B1 to an exponential over a range between 500 - 1000oC (also in GaN ML/s). Then Eq. B1 becomes:
 (B3)
(B3)
where Delta H is the enthalpy of vaporization of Ga and 1/tau0 is an attempt frequency. Hence at a given incoming Ga flux, the lowest possible surface temperature to avoid Ga condensation is given by:
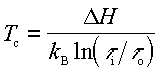 (B4)
(B4)
here Delta H is 2.71 eV, tau0 = 4.43x10-14 s/ML, and taui is the time it would take to form one ML of GaN on a (0001) plane assuming complete Ga incorporation. Thus once the Ga source is calibrated, the surface temperature can be determined by finding the temperature at which Ga condenses, using either RHEED or DMS.
[1] S. N. Mohammad, A. A. Salvador, and H. D. Morkoc, Proceedings of the IEEE 83, 1306 (1995)
[2] S. Strite, M.E. Lin, and H. Morkoc, Thin Solid Films, 231, 197 (1993)
[3] R. F. Davis, Journal of Crystal Growth 137, 161 (1994)
[4] S. Strite, H. Morkoc, J. Vac. Sci. Technol. B 10, 1237-1266 (1992).
[5] N.-E. Lee, R. C. Powell, Y.-W. Kim, J. E. Greene , J. Vac. Sci. Technol. A 13, 2293-2302 (1995).
[6] C.R. Jones, T. Lei, R. Kaspi, and K.R. Evans, Mat. Res. Symp. Proc. 395, 141 (1996)
[7] N. Newman, J. Ross, M. Rubin , Appl. Phys. Lett. 62, 1242-1244 (1993).
[8] R. Held, S.M. Seutter, B. Ishaug, A. Parkhomovsky, A.M. Dabiran, P.I. Cohen, C.J. Palmstrom , G. Nowak, I. Grzegory, and S. Porowski, J. of Cryst. Growth, to be submitted, (1998).
[9] A. R. Smith, R. M. Feenstra, D. W. Greve, J. Neugebauer, and J. E. Northrup, Phys. Rev. Lett., 79, 3934 (1997)
[10] Z. Liliental-Weber, C. Kisielowski, S. Ruvimov, Y. Chen, J. Washburn, I. Grzegory, M. Bockowski, J. Jun, and S. Porowski, j. Electron. Mater. 25 1545 (1996).
[11] R. Held, D.E. Crawford, A.M. Johnston, A.M. Dabiran, and P.I. Cohen, Journal of Electronic Materials, 26, 272 (1997)
[12] R. Held, D.E. Crawford, A.M. Johnston, A.M. Dabiran, and P.I. Cohen, presented at the MRS Fall Meeting, Boston (1996)
[13] H. Reichert, R. Averbeck, A. Graber, M. Schienle, U. Strauss, H. Thews, Mater. Res. Soc. Symp. Proc., 449, 149 (1997)
[14] D.E. Crawford, R. Held, A.M. Johnston, A.M. Dabiran, and P.I. Cohen, MRS Internet Journal of Nitride Semiconductor Research, 1, 12 (1996)
[15] Z. Yu, S. L. Buczkowski, N. C. Giles, T. H. Myers, M. R. Richards-Babb, Appl. Phys. Lett., 69, 2731 (1996)
[16] J.Y. Tsao, T.M. Brennan, and B.E. Hammons, Appl. Phys. Lett., 53, 288 (1988)
[17] W. T. Taferner, A. Bensaoula, E. Kim, and A. Bousetta, J. Vac. Sci. Technol. B 14, 2357 (1996)
[18] S. Guha, N. A. Bojarczuk, and D. W. Kisler, Appl. Phys. Lett. 69, 2879 (1996)
[19] L.K. Li, Z. Yang, W.I. Wang, Electron. Lett., 31, 2127 (1995)
[20] Y. Moriyasu, H. Goto, N. Kuze, M. Matsui, J. Cryst. Growth, 150, 916 (1995)
[21] For these data the Ga desorption measurements above condensation were done quickly, without waiting for the smoothest morphology before the measurements were made. Hence just above condensation the actual difference in Ga desorption with and without NH3 should not be used to extract growth rates.
[22] Z. Munir and A. Searcy, J. Chem. Phys. 42, 4223 (1965).
[23] D.E. Crawford, R. Held, A.M. Johnston, A.M. Dabiran, and P.I. Cohen, to be published
[24] R. C. Powell, N.-E. Lee, Y.-W. Kim, J. E. Greene, J. Appl. Phys. 73, 189-204 (1993).
[25] S. S. Liu, D. A. Stevenson, J. Electrochem.Soc. 125, 1161 (1978).
[26] CRC Handbook of Chemistry and Physics, 71st Edition, Editor-in-Chief David R. Lide, CRC Press, Boca Raton, p. 5-70 (1990)
[27] L. T. Romano and T. H. Myers, Appl. Phys. Lett., 71, 3486 (1997)
[28] S. Nakamura, Jpn. J. Appl. Phys., Part 1, 30, 1620 (1991)

Fig. 1: Schematic diagram of the Gen II MBE system used for growth.

Fig. 2: A 500x500 nm AFM image of an atomically smooth Al2O3 substrate after being cleaned in acetone and methanol, followed by an etch in 1:1 H3PO4:H2SO4. Each step was performed at 65oC for 5 min, followed by a final deionized water rinse and rapid drying with high purity N2. The steps are about 1000 Angstrom in width.

Fig. 3: Sample holder to accommodate samples stress free of any shape and size, from 3x3 mm to 1/2x1/2''. This is accomplished by 4 notched interleaving sliders mounted into a standard Varian GEN II sample block.

Fig. 4: RHEED patterns with the incident beam along the <1120> azimuth and AFM images for both NH3 and Ga-limited growth. The AFM scans cover an area of 2x2um with a z-range of 50 Angstrom and 1000 Angstrom, respectively. NH3-limited growth gives rise to a streaky RHEED pattern (a) and AFM shows atomic steps on islands (c). Ga-limited growth results in a RHEED pattern with a strong transmission component (b) and AFM indicates that this is due to facets (d). Note that for high Ga:NH3 ratios pinholes with diameters of approximately 1000 Angstrom are observed.

Fig. 5: GaN monolayer (c/2) RHEED intensity oscillations observed by first growing in the NH3-limited regime until the RHEED pattern was streaky. Then the Ga shutter was closed, the NH3 flux increased to provide Ga-limited conditions, and the substrate temperature lowered from 800oC to 670oC. Upon opening of the Ga shutter RHEED intensity oscillations were observable, recorded along the <1120> azimuth. Prolonged growth resulted in a 3-D RHEED pattern. The film is best recovered by growth in the NH3-limited regime.

Fig. 6: Intensity variation of the specular RHEED beam along the <1120>azimuth during opening and closing of the Ga shutter in an NH3 flux for (a) above, (b) at, and (c) below the condensation temperature. Curve (a) corresponds to a partial layer of weakly adsorbed Ga and partial nitridation, curve (b) to a complete layer of weakly adsorbed Ga, and curve (c) to Ga condensation.
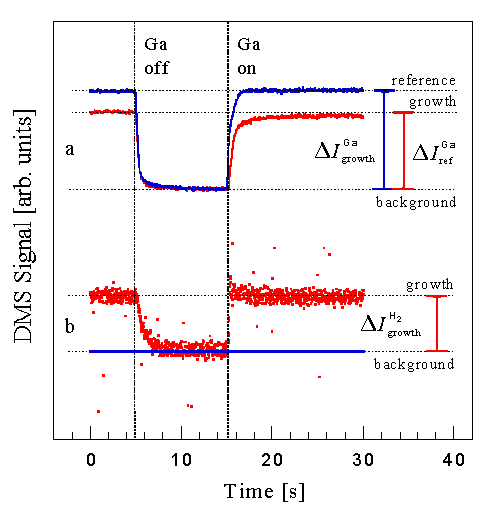
Fig. 7: Typical uncollimated Ga and H2 DMS signal during closing and opening of the Ga shutter. The growth and reference signal is obtained by measuring the rapid change in signal after closing the Ga shutter to avoid contributions of the slowly varying background signal from other cooler parts of the system. Growth rates are obtained from the Ga signals by calculating the incorporation fraction and multiplying by the known incident flux. The H2 signal was found to be proportional to the growth rate. Note that the growth rate is obtained by closing the Ga shutter instead of opening to ensure steady state after 15 min of growth.
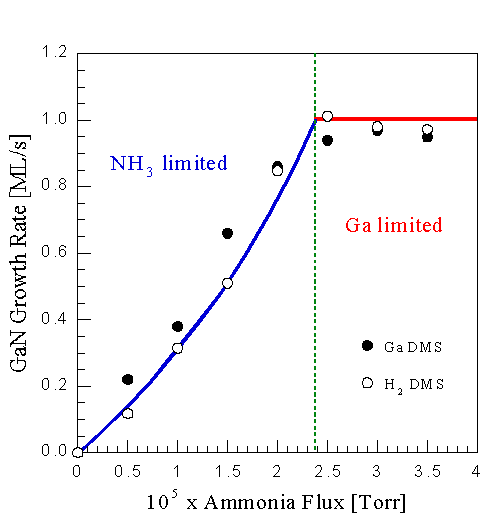
Fig. 8: GaN growth rate as a function of NH3 flux at constant Ga flux of 1.0 ML/s (GaN) and surface temperature of 785oC, using both the Ga and H2 signal. Both growth regimes can be identified, NH3-limited and Ga-limited. In the NH3-limited regime the growth rate is an approximately linear function of the NH3 flux, while in the Ga-limited regime near unity Ga incorporation is obtained. Note the good agreement between using Ga and H2 DMS.

Fig. 9: GaN growth rate as a function of Ga flux at constant NH3 flux of 1.0x10-5 Torr and surface temperature of 785oC, using Ga DMS. Two growth regimes can be identified, Ga-limited and NH3-limited. Near unity incorporation of Ga is obtained during Ga-limited growth. During NH3-limited growth the growth rate reduces as a function of Ga flux, approaching zero at the flux required for condensation at this temperature. This reduction is attributed to weakly adsorbed Ga blocking active Ga terminated GaN sites.
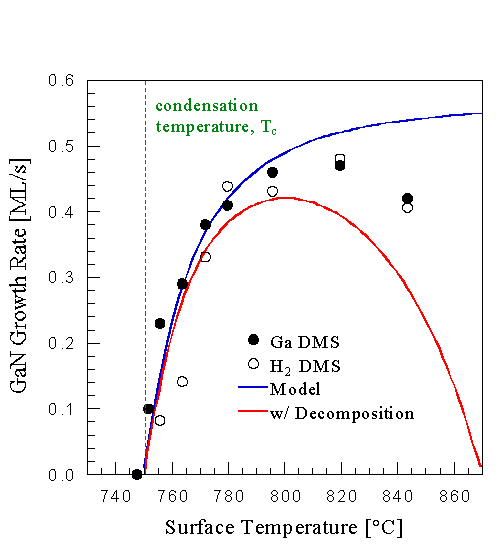
Fig. 10: GaN growth rate as a function of surface temperature at constant Ga flux of 1.0 ML/s (GaN) and NH3 flux of 1.0x10-5 Torr, using both the Ga and H2 signal. The growth rate reduces towards the condensation temperature, attributed to weakly adsorbed Ga blocking active Ga terminated GaN sites. The high temperature growth rate reduction is due to GaN decomposition competing with growth.

Fig. 11: AlN RHEED intensity oscillations were observed by preparing a GaN surface in the NH3-limited regime similar as for GaN oscillations. So far we were not able to smooth an AlN surface sufficiently to obtain AlN oscillation from an initial AlN surface. To our knowledge this is the first report of AlN oscillations.

Fig. 12: GaN RHEED intensity oscillations at the low temperature limit show a linear increase in oscillation frequency as a function of Ga flux. The frequency does not quite correspond to monolayer growth. The slope is roughly 0.9, and an offset is observed. This offset increases with increasing NH3 flux.
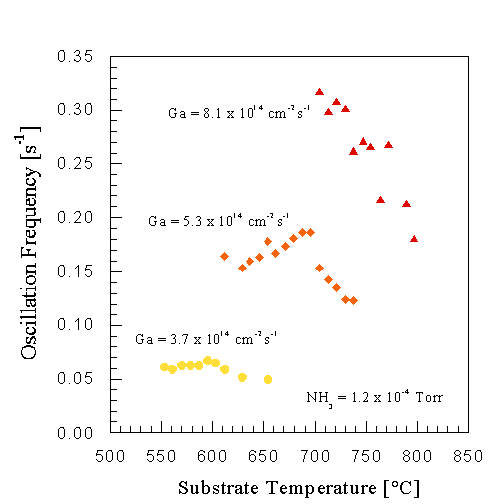
Fig. 13: GaN RHEED intensity oscillation frequency as a function of sample temperature for different Ga fluxes. The decrease in oscillation frequency at higher temperatures is attributed to a transition from island nucleation to step flow growth. The activcation energy of this process was found to be 1.2 eV.

Fig. 14: RHEED and uncollimated Ga DMS signal without NH3 flux above the condensation temperature. Level 1 indicates a nitrided starting surface, while a stable level 2 is reached after Ga exposure, indicating a Ga terminated surface. Note that during Ga exposure the intensity level reaches steady state below level 2 suggesting fractional coverage of weakly adsorbed Ga.

Fig. 15: The transient response of the Ga and H2 desorption to a step-function of incident Ga is shown in the absence of incident NH3. The response of the specular RHEED intensity observed along the <1120> azimuth is also shown. FGa = 1.6x1015 cm-2s-1, Tsub = 760oC).

Fig. 16: Specular RHEED intensity and its first derivative. Differentiation of the signal allows quantitative analysis of the transient signal. Experimental conditions for the data shown here are Tsub = 780oC, NH3 BEP=1.1x10-5 Torr. FGa = 1.45ML/s.
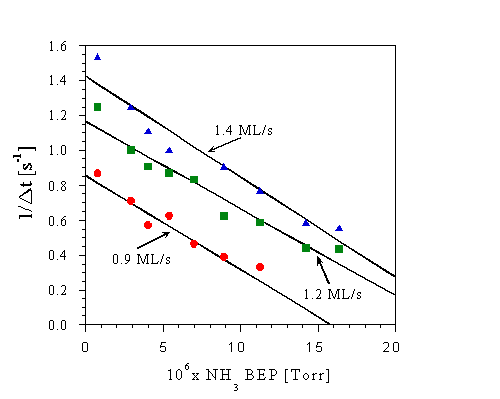
Fig. 17: Dependence of the surface transformation rate, 1/Delta t, on incident NH3 BEP. Substrate temperature is 780oC. The linear curve fits shown in the figure were obtained using the least-squares method.
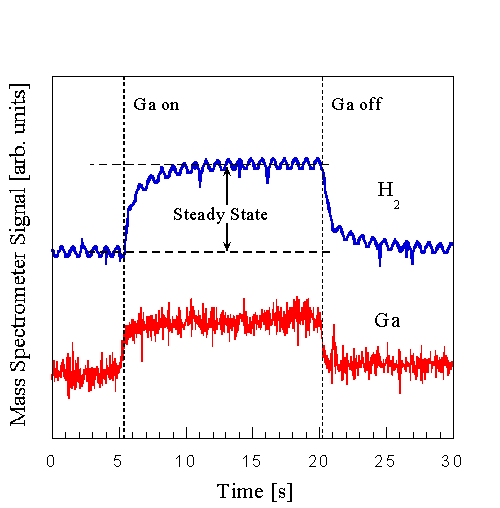
Fig. 18: Changes in the H2 and Ga desorption are caused by exposing a smooth GaN sample to a 15 second pulse of incident Ga under excess NH3 conditions. Tsub = 820oC, NH3 BEP = 7x10-6 Torr, FGa = 4.2x1014 cm-2s-1 . The high frequency H2 signal oscillations arise from fluctuations in H2 background pressure caused by temperature cycling of the cryopumps.

Fig. 19: Changes in the H2 and Ga desorption are caused by exposing a smooth GaN sample to a 15 second pulse of incident Ga under excess Ga conditions. Tsub = 820oC, NH3 BEP = 7x10-6 Torr, FGa =1.4x1015 cm-2s-1. The H2 signal oscillations arise from fluctuations in H2 background pressure caused by temperature cycling of the cryopumps. Note the pulse in the H2 signal after opening and closing the Ga shutter.
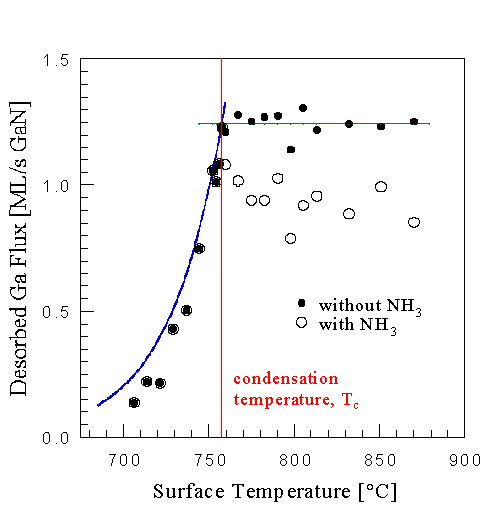
Fig. 20: Condensation temperature determination using collimated Ga DMS with and without NH3 for an incident Ga flux of 1.25 ML/s GaN. Without NH3 the DMS signal remains constant above the condensation temperature, while with NH3 the signal is reduced due to GaN formation. The condensation temperature is found as illustrated by observing the temperature at which the signal drops exponentially. No growth is observed below the condensation temperature. The solid curve at temperatures below Tc is calculated from Ga vapor pressure data, closely followed by the experimental data. (The data presented in this figure should not be used for growth rate determination since steady state was not obtained.)
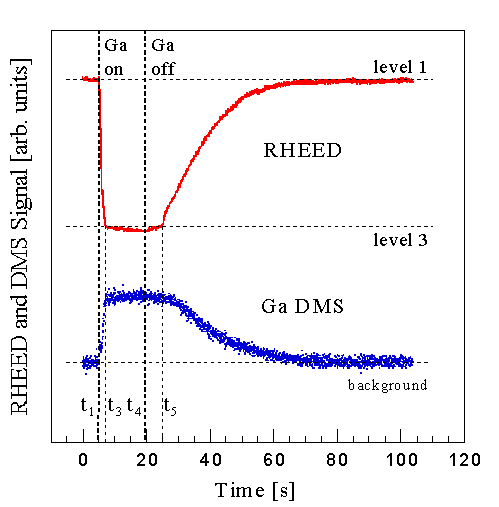
Fig. 21: RHEED and uncollimated Ga DMS signal during Ga accumulation below the condensation temperature. After the Ga shutter is closed at t4 Ga desorption remains constant until part of the GaN surface is exposed at t5. At the same time, the RHEED intensity increases slowly up to t5 where a large change in slope takes place. The slow decrease of the DMS signal after t5 is partly due to the temperature gradient across the sample, resulting in unsynchronized completion of Ga desorption from the surface.

Fig. 22: The rate of GaN decomposition compared with values previously reported by Munir and Searcy. The data presented here extends the experimental curve to lower temperatures. The current measured on the mass spectrometer while monitoring desorption of molecular nitrogen was multiplied by a constant factor such that the signals are equal in the middle of the range of measured values. The close agreement between the activation energies of the 1/2 N2 curve and the Ga curve indicate that decomposition is congruent.
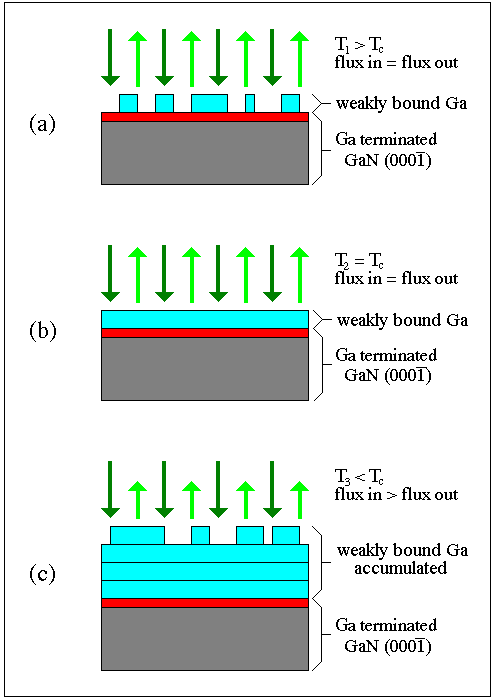
Fig. 23: Behavior of incident Ga on a rigidly attached (strongly bound) Ga termination layer as a function of temperature in the absence of NH3 Above the condensation temperature (a) steady state partial Ga coverage is obtained, and the incident flux equals the desorbing flux. Complete steady state Ga coverage is obtained at a critical temperature (b) below which Ga condensation takes place. Note that the incident flux still equals the desorbing flux. Below this critical temperature (c), Ga multilayer accumulation takes place and the incident flux exceeds the desorbing flux.
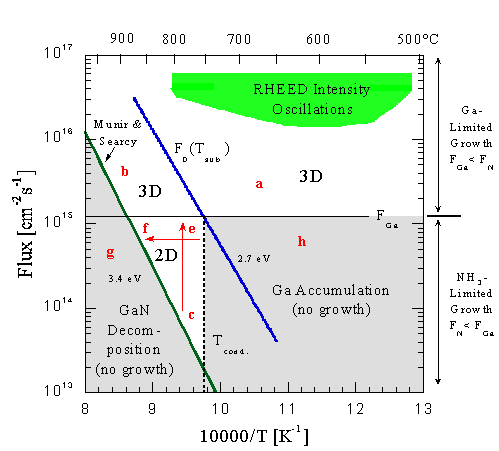
Fig. 24: GaN growth map showing the different growth regimes and limits for a fixed Ga flux. Growth is limited by GaN decomposition at high temperatures and Ga accumulation in the NH3-limited regime at low temperatures. 3-D growth occurs in the Ga-limited regime, while layer-by-layer growth takes place in the NH3-limited regime between the GaN decomposition and Ga accumulation limits. Strong GaN RHEED intensity oscillations are observed by first growing in the NH3-limited regime until a streaky RHEED pattern is obtained, followed by growth in the Ga-limited regime.
Back to my home page